案例背景

好久没做这种机器学习全流程的案例了，毕竟我是靠这个起家的，最近重温一下吧。很多新手或者是刚入门的同学可以凭借这个案例学一下机器学习。

本次案例是一个价格预测，它是一个连续型的变量，因此它是一个回归问题。所以这是一篇回归问题的全流程的代码。从数据清洗到特征工程到分析可视化，再到模型选择，模型训练，交叉验证，超参数搜索，有效性评估，非常多的流程和套路。

数据介绍

本次做汽车价格的预测呢主要就是一些汽车的一些特征，牌子，年份什么的。主要变量有下面这些。

46022条数据，数据量挺大的作，作为一般的机器学习模型来说，这种数据量已经能够训练出较为准确的模型了。

目标就是做到输入这些特征，然后就能输出这个汽车的价格，保证准确率很高。

变量不是很多，因此进行学习和作业是一个很不错的案例。

当然需要所有的代码文件和本次案例数据的同学还是可以参考：汽车价格预测。

代码实现

读取数据

还是先导入数据科学常用的包

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt 
import seaborn as sns

plt.rcParams ['font.sans-serif'] ='SimHei'               #显示中文
plt.rcParams ['axes.unicode_minus']=False               #显示负号

读取数据查看信息

df=pd.read_csv('Clean Data_pakwheels.csv')
df=df[[col for col in df.columns if 'Unnamed' not in col]]
df.head(2)

查看数据基础信息

df.info()

观察变量缺失值情况

#观察缺失值
import missingno as msno
msno.matrix(df)

没有缺失值，直接开始特征工程

数据预处理

#查看数值型数据,
pd.set_option('display.max_columns', 30)
df.select_dtypes(exclude=['object']).head()

Price作为响应变量y，Model Year转为车龄age，其他变量不用处理

y=df['Price']; df['age']=2024-df['Model Year']

#查看非数值型数据

df.select_dtypes(exclude=['int64','float64']).head()

查看一下这些类别变量的取值类别数量都有多少


for col in df.select_dtypes(exclude=['int64','float64']).columns:
    print(f'{col}特征类别数量为{len(df[col].unique())}')

其中，

  • Model Name特征变量类别太多，进行删除。

  • 颜色24类有很多类似的颜色可以进行归类，减少变量。

  • Silver/Grey: 包括银色和灰色。

  • White/Beige: 包括白色和米色。

  • Black: 只包括黑色。

  • Brown系: 包括棕色、栗色、褐红色和铜色。

  • Gold: 只包括金色。

  • Blue系: 包括蓝色、海军蓝和靛蓝。

  • Red系: 包括红色、粉色、洋红和酒红色。

  • Green系: 包括绿色和绿松石色。

  • Orange: 只包括橙色。

  • Purple: 只包括紫色。

  • Yellow: 只包括黄色。

  • Unlisted: 包括未列出的颜色。

  • Company Name特征类别数量为31，也要进行适当的归类处理

df=df.drop(columns=['Model Name'])

进行颜色的映射

color_mapping = {
    'Silver': ['Silver', 'Grey'],
    'White': ['White', 'Beige'],
    'Black': ['Black'],
    'Brown': ['Brown', 'Maroon', 'Burgundy', 'Bronze'],
    'Gold': ['Gold'],
    'Blue': ['Blue', 'Navy', 'Indigo'],
    'Red': ['Red', 'Pink', 'Magenta', 'Wine'],
    'Green': ['Green', 'Turquoise'],
    'Orange': ['Orange'],
    'Purple': ['Purple'],
    'Yellow': ['Yellow'],
    'Unlisted': ['Unlisted', 'Assembly']  
}
inverse_color_mapping = {val: key for key, vals in color_mapping.items() for val in vals}
# 映射
df['Color'] = df['Color'].map(inverse_color_mapping)
print(len(df['Color'].unique()))

### 等同下面这个方法

inverse_color_mapping = {}

# 对原始字典进行双重循环
for main_color, variations in color_mapping.items():
    for color in variations:
        # 将变体颜色作为键，主要颜色作为值添加到字典中
        inverse_color_mapping[color] = main_color
inverse_color_mapping

颜色类别减少为12，下面对汽车品牌处理

c=df['Company Name'].value_counts()  # 统计每个品牌车辆的样本数量，然后计算每个品牌车辆的均价
df.groupby(['Company Name']).mean(numeric_only=True).loc[c.index,:].assign(count=c.to_numpy())[['Price','count']].style.bar(align='mid', color=['#491256', 'skyblue'])

Suzuki，Toyota，Honda，Daihatsu四个品牌已经大概包含了大部分车辆，其他的剩下面的车辆可以归为一类， 但是有些牌子可能是奢侈品豪车，均价超级贵，所以我们把下面的Price均价分为三个区间，0-100w的作为普通其他类，100w-500w作为中档其他类，500w以上为高档其他类。

c_p=df.groupby(['Company Name']).mean(numeric_only=True).loc[c.index,:]['Price'].iloc[4:]
print(f'普通其他类:{c_p[c_p<1000000].index}')
print(f'中档其他类:{c_p[(c_p > 1000000) & (c_p < 5000000)].index}')
print(f'高档其他类:{c_p[c_p>5000000].index}')

映射处理

brand_mapping = {
    'Suzuki': 'Suzuki',
    'Toyota': 'Toyota',
    'Honda': 'Honda',
    'Daihatsu': 'Daihatsu',   #这四个牌子保留
    'General': ['Hyundai', 'United', 'Daewoo', 'Chevrolet', 'Chery', 'Fiat', 'Adam'],
    'Mid-Range': ['Nissan', 'Mitsubishi', 'FAW', 'Mazda', 'KIA', 'Subaru', 'SsangYong', 'Land', 'DFSK', 'Jeep', 'MINI', 'Volvo'],
    'Premium': ['Mercedes', 'Audi', 'BMW', 'Lexus', 'Range', 'Porsche', 'Hummer', 'Jaguar'] }
# Inverting the mapping
inverse_brand_mapping = {val: key for key, vals in brand_mapping.items() for val in ([vals] if isinstance(vals, str) else vals)}
df['Company Name'] = df['Company Name'].map(inverse_brand_mapping, na_action='ignore')  # na_action='ignore' to keep the original value if not found in mapping
print(len(df['Company Name'].unique()))

也可以下面这样做

### 等同下面这个方法
inverse_brand_mapping = {}

# 对原始字典进行双重循环
for brand, models in brand_mapping.items():
    # 检查models是否是字符串类型，如果是，将其转换为列表
    if isinstance(models, str):
        models = [models]
    # 遍历模型列表
    for model in models:
        # 将牌子作为键，品牌作为值添加到字典中
        inverse_brand_mapping[model] = brand
inverse_brand_mapping

处理完成之后，我们再来检查一下特征类别的数量。

for col in df.select_dtypes(exclude=['int64','float64']).columns:
    print(f'{col}特征类别数量为{len(df[col].unique())}')

再把响应变量从x里面排除

df=df.drop(columns=['Price'])

画图！

数据画图探索

数值型变量画图

#查看特征变量的箱线图分布
num_columns = df.select_dtypes(exclude=['object']).columns.tolist() # 列表头
dis_cols = 2                   #一行几个
dis_rows = len(num_columns)
plt.figure(figsize=(3 * dis_cols, 2.5 * dis_rows),dpi=128)
 
for i in range(len(num_columns)):
    plt.subplot(dis_rows,dis_cols,i+1)
    sns.boxplot(data=df[num_columns[i]], orient="v",width=0.5)
    plt.xlabel(num_columns[i],fontsize = 16)
plt.tight_layout()
#plt.savefig('特征变量箱线图',formate='png',dpi=500)
plt.show()

车龄存在一些极大异常值，有一些车车龄很大。Mileage ，engine capacity 也有很多极大值。

型号年份（Model Year）：大部分车辆的型号年份集中在2005年到2015年之间，中位数大约在2010年左右。这表明大多数车辆相对较新。箱线图下方的长尾表明也有少量较旧的车辆，但这些较老的车辆相对不多。

里程（Mileage）：大多数车辆的里程较低，中位数接近0，但范围广泛，上至100万公里。这说明有些车辆使用非常频繁，但大多数车辆保持较低的里程数。长尾分布表明有些车辆的里程异常高，这可能反映了部分车辆经受了长期的使用。

引擎容量（Engine Capacity）：大部分车辆的引擎容量在0到2000cc之间，中位数在1000cc到1500cc左右。这表明大多数车辆装配的是中小型引擎。存在一些异常点，表明有少量车辆装配了非常小或非常大的引擎。 车龄（Age）：车龄的分布显示，大多数车辆的年龄集中在5到15年之间，中位数约为10年。这意味着大多数车辆都不是很新，但也未达到极老的状态。和型号年份的分析相符，说明市场上流通的车辆大多数都有一定的使用历史。

#画密度图，训练集和测试集对比
dis_cols = 2                   #一行几个
dis_rows = len(num_columns)
plt.figure(figsize=(3 * dis_cols, 2 * dis_rows),dpi=256)
 
for i in range(len(num_columns)):
    ax = plt.subplot(dis_rows, dis_cols, i+1)
    ax = sns.kdeplot(df[num_columns[i]], color="skyblue" ,fill=True)
    ax.set_xlabel(num_columns[i],fontsize = 14)
plt.tight_layout()
#plt.savefig('训练测试特征变量核密度图',formate='png',dpi=500)
plt.show()

和上面结论一致，age ， Mileage ，engine capacity ，典型的右偏分布 存在很多极大值。

分类型变量画图

df.select_dtypes(exclude=['int64','float64']).columns

画柱状图

# Select non-numeric columns
non_numeric_columns = df.select_dtypes(exclude=['int64', 'float64']).columns
# Set up the matplotlib figure with 2x4 subplots
f, axes = plt.subplots(4, 2, figsize=(10,12),dpi=128)
# Flatten axes for easy iterating
axes_flat = axes.flatten()
# Loop through the non-numeric columns and create a countplot for each
for i, column in enumerate(non_numeric_columns):
    if i < 8:  # Check to avoid IndexError if there are more than 8 non-numeric columns
        sns.countplot(x=column, data=df, ax=axes_flat[i])
        axes_flat[i].set_title(f'Count of {column}')
        for label in axes_flat[i].get_xticklabels():
            label.set_rotation(45)

# Hide any unused subplots
for j in range(i + 1, 8):
    f.delaxes(axes_flat[j])
plt.tight_layout()
plt.show()

公司名称：图表显示Toyota和Suzuki是数量最多的品牌，其次是Honda。这可能表明在相关市场中，Toyota和Suzuki更受欢迎，可能因为它们的可靠性、品牌认知度或性价比。Premium（可能代表高端品牌）和General（可能代表普通或非专门品牌）的数量明显少于前三者，这表明市场可能更倾向于具有中等价格和质量的车辆。

地点：该图展示了汽车的地理分布情况。伊斯兰堡（Islamabad）的数量最多，其次是旁遮普省（Punjab）。这可能反映了这些区域的高车辆需求或更高的购买力。

引擎类型：绝大多数车辆使用的是汽油（Petrol）引擎，而柴油（Diesel）和混合动力（Hybrid）引擎的车辆数量相对较少。这可能是由于汽油车的普及度高，以及在某些地区对于柴油和混合动力车的支持不足。

颜色：银色（Silver）和白色（White）车辆在数量上占据优势，这可能因为这些颜色的车辆更受欢迎，也可能与热量反射能力或经典美观有关。未上市（Unlisted）颜色的数量相对较少，可能包含特殊或定制的颜色。

装配类型：本地装配（Local）的车辆远多于进口车辆（Imported）。这可能反映了本地制造车辆的成本优势或进口税的影响。

车身类型：轿车（Sedan）和掀背车（Hatchback）是最常见的车身类型，而SUV的数量相对较少。这可能反映了市场上对于日常使用和经济型车辆的高需求。

变速器类型：自动档（Automatic）车辆数量少于手动档（Manual）车辆，这可能与成本、驾驶习惯或车辆类型有关。

注册状态：已注册（Registered）的车辆数量远超未注册（Un-Registered）的车辆，这显示了大多数车辆在使用前已完成了注册流程。

响应变量y的分布

# 查看y的分布
#回归问题
plt.figure(figsize=(7,3),dpi=128)
plt.subplot(1,3,1)
y.plot.box(title='响应变量箱线图')
plt.subplot(1,3,2)
y.plot.hist(title='响应变量直方图')
plt.subplot(1,3,3)
y.plot.kde(title='响应变量核密度图')
#sns.kdeplot(y, color='Red', shade=True)
#plt.savefig('响应变量.png')
plt.tight_layout()
plt.show()

有些车的价格异常值太夸张，处理一下

#处理y的异常值  二千万以上的车就去掉
y=y[y <= 20000000]
plt.figure(figsize=(7,3),dpi=128)
plt.subplot(1,3,1)
y.plot.box(title='响应变量箱线图')
plt.subplot(1,3,2)
y.plot.hist(title='响应变量直方图')
plt.subplot(1,3,3)
y.plot.kde(title='响应变量核密度图')
#sns.kdeplot(y, color='Red', shade=True)
#plt.savefig('响应变量.png')
plt.tight_layout()
plt.show()

可以看到极端异常值被我们塞掉了，将处理的变量的样本索引给x

#筛选给x
df=df.iloc[y.index,:]
print(f'删除了样本数量：{46022-df.shape[0]}')
df.shape

X异常值处理

为了统一展示x的分布，我们将其进行一个标准化。注意，我们这里对x进行了一个独立热编码，也就是把类别变量都拆成了很多列，一个类别都拆成一条变量。

#X变量独热处理
X=pd.get_dummies(df)
#X异常值处理，先标准化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_s = scaler.fit_transform(X)

 然后画图查看

plt.figure(figsize=(20,8),dpi=128)
plt.boxplot(x=X_s,labels=X.columns)
plt.hlines([-10,10],0,len(X.columns))
plt.xticks(rotation=90)
plt.show()

蓝色的线是10倍的方差，可以看到很多x他们居然都在均值10倍方差之外，这种异常值肯定是得进行剔除的，不然会影响模型的性能。

样本个体数据方大于整体数据10倍的标准差之外就筛掉。

#异常值多的列进行处理
def deal_outline(data,col,n):   #数据，要处理的列名，几倍的方差
    for c in col:
        mean=data[c].mean()
        std=data[c].std()
        data=data[(data[c]>mean-n*std)&(data[c]<mean+n*std)]
        #print(data.shape)
    return data
X=deal_outline(X,X.columns,10)  #筛掉异常值

 #取值唯一的独热变量删除

#取值唯一的独热变量删除
for col in X.columns:
    if len(X[col].value_counts())==1:
        print(col)
        X.drop(col,axis=1,inplace=True)
y=y[X.index]
print(f'删除了样本数量：{df.shape[0]-X.shape[0]}')
X.shape,y.shape

现在我们还剩下4.49万的样本。

相关系数矩阵

我们可以画出变量两两之间的相关性热力图但是变量独热之后有点多，就不把颜色和车身类型等变量放上去了。

#变量独热之后有点多，就不把颜色和车身类型等变量放上去了
X_plot=X[[col for col in X.columns if 'Color' not in col]]
X_plot=X_plot[[col for col in X_plot.columns if 'Body' not in col]]

画图

corr = plt.subplots(figsize = (18,16),dpi=128)
corr= sns.heatmap(X_plot.assign(Y=y).corr(method='spearman'),annot=True,square=True)

 

明显的负相关关系：一些变量对显示为深紫色，表示它们之间存在较强的负相关。例如，“Mileage”和“Engine Capacity”之间似乎有一定的负相关性，这可能意味着发动机容量越大，车辆的里程数越少，这是有意义的，因为大发动机通常消耗更多的燃料。

明显的正相关关系：一些变量对显示为深红色，指示它们之间存在强烈的正相关。例如，“Engine Type_Petrol”和“Company Name_General”可能有较高的正相关，这可能意味着某个特定的汽车制造商更倾向于生产汽油发动机车型。

弱相关或无相关关系：很多变量对显示为接近黑色，表示它们之间几乎没有或没有明显的相关性。这表明很多车辆特征之间可能没有直接的或显著的影响关系。

特定地区或特征的相关性：可以注意到某些特定区域（如Location_JK, Location_Punjab等）和其他变量之间存在不同程度的相关性。这可能表明地区因素对车辆的某些属性有影响，例如某一地区可能更倾向于特定类型的车辆或发动机类型。

开始机器学习

#划分训练集和验证集
from sklearn.model_selection import train_test_split
X_train,X_val,y_train,y_val=train_test_split(X,y,test_size=0.2,random_state=0)

然后标准化

#数据标准化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train_s = scaler.transform(X_train)
X_val_s = scaler.transform(X_val)
print('训练数据形状：')
print(X_train_s.shape,y_train.shape)
print('验证数据形状：')
(X_val_s.shape,y_val.shape,)

可以看到还有三十九个变量，训练集大概有3.5w条，测试机大概有9k条

模型选择

又到了常见的对比套路环节了，基本上我都是10种机器学习模型做对比。

#采用十种模型，对比验证集精度
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import ElasticNet
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from xgboost.sklearn import XGBRegressor
from lightgbm import LGBMRegressor
from sklearn.svm import SVR
from sklearn.neural_network import MLPRegressor

实例化

#线性回归
model1 = LinearRegression()
 
#弹性网回归
model2 = ElasticNet(alpha=0.05, l1_ratio=0.5)
 
#K近邻
model3 = KNeighborsRegressor(n_neighbors=10)
 
#决策树
model4 = DecisionTreeRegressor(random_state=77)
 
#随机森林
model5= RandomForestRegressor(n_estimators=500,  max_features=int(X_train.shape[1]/3) , random_state=0)
 
#梯度提升
model6 = GradientBoostingRegressor(n_estimators=500,random_state=123)
 
#极端梯度提升
model7 =  XGBRegressor(objective='reg:squarederror', n_estimators=1000, random_state=0)
 
#轻量梯度提升
model8 = LGBMRegressor(n_estimators=1000,objective='regression', # 默认是二分类
                      random_state=0,force_row_wise=True)
 
#支持向量机
model9 = SVR(kernel="rbf")
 
#神经网络
model10 = MLPRegressor(hidden_layer_sizes=(16,8), random_state=77, max_iter=10000)
 
model_list=[model1,model2,model3,model4,model5,model6,model7,model8,model9,model10]
model_name=['线性回归','惩罚回归','K近邻','决策树','随机森林','梯度提升','极端梯度提升','轻量梯度提升','支持向量机','神经网络']

定义评价指标

from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error,r2_score
 
def evaluation(y_test, y_predict):
    mae = mean_absolute_error(y_test, y_predict)
    mse = mean_squared_error(y_test, y_predict)
    rmse = np.sqrt(mean_squared_error(y_test, y_predict))
    mape=(abs(y_predict -y_test)/ y_test).mean()
    r_2=r2_score(y_test, y_predict)
    return mae, rmse, mape,r_2  #mse

训练拟合对比

df_eval=pd.DataFrame(columns=['MAE','RMSE','MAPE','R2'])
for i in range(len(model_list)):
    model_C=model_list[i]
    name=model_name[i]
    print(f'{name}正在训练...')
    model_C.fit(X_train_s, y_train)
    pred=model_C.predict(X_val_s)
    s=evaluation(y_val,pred)
    df_eval.loc[name,:]=list(s)

查看评价指标

df_eval

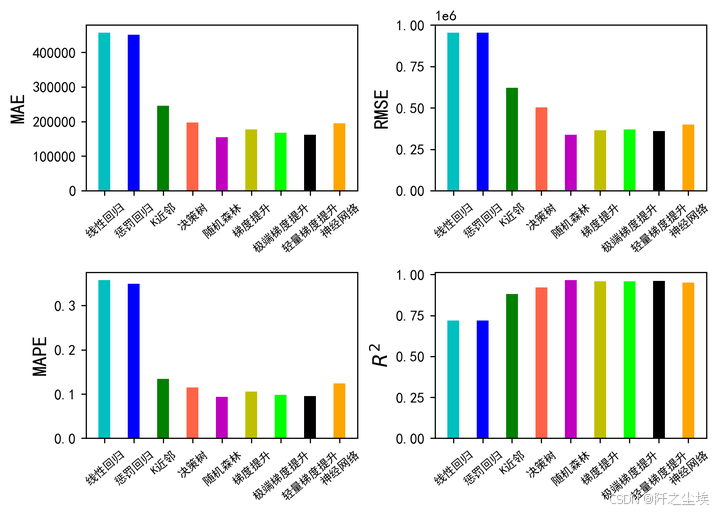
看表格可能不直观，我们进行可视化

bar_width = 0.4
colors=['c', 'b', 'g', 'tomato', 'm', 'y', 'lime', 'k','orange','pink','grey','tan','purple']
fig, ax = plt.subplots(2,2,figsize=(7,5),dpi=256)
for i,col in enumerate(df_eval.columns):
    n=int(str('22')+str(i+1))
    plt.subplot(n)
    df_col=df_eval[col]
    m =np.arange(len(df_col))
    
    #hatch=['-','/','+','x'],
    plt.bar(x=m,height=df_col.to_numpy(),width=bar_width,color=colors)
    
    #plt.xlabel('Methods',fontsize=12)
    names=df_col.index
    plt.xticks(range(len(df_col)),names,fontsize=8)
    plt.xticks(rotation=40)
    
    if col=='R2':
        plt.ylabel(r'$R^{2}$',fontsize=14)
    else:
        plt.ylabel(col,fontsize=14)
plt.tight_layout()
#plt.savefig('柱状图.jpg',dpi=512)
plt.show()

支持向量机太差劲了.去掉画图

df_eval2=df_eval.loc[['线性回归', '惩罚回归', 'K近邻', '决策树', '随机森林', '梯度提升', '极端梯度提升', '轻量梯度提升','神经网络'],:]

bar_width = 0.4
colors=['c', 'b', 'g', 'tomato', 'm', 'y', 'lime', 'k','orange','pink','grey','tan','purple']
fig, ax = plt.subplots(2,2,figsize=(7,5),dpi=256)
for i,col in enumerate(df_eval.columns):
    n=int(str('22')+str(i+1))
    plt.subplot(n)
    df_col=df_eval2[col]
    m =np.arange(len(df_col))
    
    #hatch=['-','/','+','x'],
    plt.bar(x=m,height=df_col.to_numpy(),width=bar_width,color=colors)
    
    #plt.xlabel('Methods',fontsize=12)
    names=df_col.index
    plt.xticks(range(len(df_col)),names,fontsize=8)
    plt.xticks(rotation=40)
    
    if col=='R2':
        plt.ylabel(r'$R^{2}$',fontsize=14)
    else:
        plt.ylabel(col,fontsize=14)
plt.tight_layout()
#plt.savefig('柱状图.jpg',dpi=512)
plt.show()

集成模型方法都是最好的，也就是XGB,LGBM,RF等。下面我们对这三个模型进行交叉验证，进一步评价他们的效果。

交叉验证

#回归问题交叉验证，使用拟合优度，mae,rmse,mape 作为评价标准
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error,r2_score
from sklearn.model_selection import KFold
 
def evaluation(y_test, y_predict):
    mae = mean_absolute_error(y_test, y_predict)
    mse = mean_squared_error(y_test, y_predict)
    rmse = np.sqrt(mean_squared_error(y_test, y_predict))
    mape=(abs(y_predict -y_test)/ y_test).mean()
    r_2=r2_score(y_test, y_predict)
    return mae, rmse, mape
def evaluation2(lis):
    array=np.array(lis)
    return array.mean() , array.std()

自定义交叉验证函数

def cross_val(model=None,X=None,Y=None,K=5,repeated=1):
    df_mean=pd.DataFrame(columns=['R2','MAE','RMSE','MAPE']) 
    df_std=pd.DataFrame(columns=['R2','MAE','RMSE','MAPE'])
    for n in range(repeated):
        print(f'正在进行第{n+1}次重复K折.....随机数种子为{n}\n')
        kf = KFold(n_splits=K, shuffle=True, random_state=n)
        R2=[]; MAE=[] ; RMSE=[]  ; MAPE=[]
        print(f"    开始本次在{K}折数据上的交叉验证.......\n")
        i=1
        for train_index, test_index in kf.split(X):
            print(f'        正在进行第{i}折的计算')
            X_train=X.values[train_index]
            y_train=y.values[train_index]
            X_test=X.values[test_index]
            y_test=y.values[test_index]
            model.fit(X_train,y_train)
            score=model.score(X_test,y_test)
            R2.append(score)
            pred=model.predict(X_test)
            mae, rmse, mape=evaluation(y_test, pred)
            MAE.append(mae)
            RMSE.append(rmse)
            MAPE.append(mape)
            print(f'        第{i}折的拟合优度为：{round(score,4)}，MAE为{round(mae,4)}，RMSE为{round(rmse,4)}，MAPE为{round(mape,4)}')
            i+=1
        print(f'    ———————————————完成本次的{K}折交叉验证———————————————————\n')
        R2_mean,R2_std=evaluation2(R2)
        MAE_mean,MAE_std=evaluation2(MAE)
        RMSE_mean,RMSE_std=evaluation2(RMSE)
        MAPE_mean,MAPE_std=evaluation2(MAPE)
        print(f'第{n+1}次重复K折，本次{K}折交叉验证的总体拟合优度均值为{R2_mean}，方差为{R2_std}')
        print(f'                               总体MAE均值为{MAE_mean}，方差为{MAE_std}')
        print(f'                               总体RMSE均值为{RMSE_mean}，方差为{RMSE_std}')
        print(f'                               总体MAPE均值为{MAPE_mean}，方差为{MAPE_std}')
        print("\n====================================================================================================================\n")
        df1=pd.DataFrame(dict(zip(['R2','MAE','RMSE','MAPE'],[R2_mean,MAE_mean,RMSE_mean,MAPE_mean])),index=[n])
        df_mean=pd.concat([df_mean,df1])
        df2=pd.DataFrame(dict(zip(['R2','MAE','RMSE','MAPE'],[R2_std,MAE_std,RMSE_std,MAPE_std])),index=[n])
        df_std=pd.concat([df_std,df2])
    return df_mean,df_std

首先对lgbm模型进行交叉验证

model = LGBMRegressor(n_estimators=1000,objective='regression',random_state=0)
lgb_crosseval,lgb_crosseval2=cross_val(model=model,X=X,Y=y,K=3,repeated=5)

这里可能是版本问题，lgbm在给我报一些警告，也不知道是啥。

然后对xgboost进行交叉验证

model = XGBRegressor(n_estimators=1000,objective='reg:squarederror',random_state=0)
xgb_crosseval,xgb_crosseval2=cross_val(model=model,X=X,Y=y,K=3,repeated=5)

这次就能很清楚的看到每次交叉验证的一个效果以及整体的效果。

还剩下随机森林的交叉验证：

model = RandomForestRegressor(n_estimators=500,  max_features=int(X_train.shape[1]/3) , random_state=0)
rf_crosseval,rf_crosseval2=cross_val(model=model,X=X,Y=y,K=3,repeated=5)

四个评价指标的均值图

plt.subplots(1,4,figsize=(16,3))
for i,col in enumerate(lgb_crosseval.columns):
    n=int(str('14')+str(i+1))
    plt.subplot(n)
    plt.plot(lgb_crosseval[col], 'k', label='LGB')
    plt.plot(xgb_crosseval[col], 'b-.', label='XGB')
    plt.plot(rf_crosseval[col], 'r-^', label='RF')
    plt.title(f'不同模型的{col}对比')
    plt.xlabel('重复交叉验证次数')
    plt.ylabel(col,fontsize=16)
    plt.legend()
plt.tight_layout()
plt.show()

四个评价指标的方差图

plt.subplots(1,4,figsize=(16,3))
for i,col in enumerate(lgb_crosseval2.columns):
    n=int(str('14')+str(i+1))
    plt.subplot(n)
    plt.plot(lgb_crosseval2[col], 'k', label='LGB')
    plt.plot(xgb_crosseval2[col], 'b-.', label='XGB')
    plt.plot(rf_crosseval2[col], 'r-^', label='RF')
    plt.title(f'不同模型的{col}方差对比')
    plt.xlabel('重复交叉验证次数')
    plt.ylabel(col,fontsize=16)
    plt.legend()
plt.tight_layout()
plt.show()

随机森林的效果最好，我们选择他作为最终的模型，下面对随机森林搜索超参数。

搜超参数

#利用K折交叉验证搜索最优超参数
from sklearn.model_selection import KFold, StratifiedKFold
from sklearn.model_selection import GridSearchCV,RandomizedSearchCV

设置

# 设置参数分布
param_distributions = {
    'n_estimators': [100, 300, 500, 800,1000],  # 树的数量
    'max_features': range(9, 15),  # 最大特征数
    'max_depth': range(8, 13),  # 最大深度
}

# 定义交叉验证
kfold = KFold(n_splits=3, shuffle=True, random_state=1)

# 初始化随机森林回归器
model = RandomForestRegressor(random_state=0)
# 使用 RandomizedSearchCV
random_search = RandomizedSearchCV(estimator=model, param_distributions=param_distributions, 
                                   n_iter=50, cv=kfold, verbose=2, random_state=0, n_jobs=-1)
# 拟合模型
random_search.fit(X_train_s, y_train)
# 打印最佳参数
print("Best parameters:", random_search.best_params_)

将最好的参数给他传进去

model = random_search.best_estimator_
model.score(X_val_s, y_val)

进行拟合和评价

model=RandomForestRegressor(n_estimators=1000,  max_features=13 ,max_depth=12, random_state=0)
model.fit(X_train_s, y_train)
model.score(X_val_s, y_val)

变量重要性排序图

我们在全部数据上进行训练。

model=RandomForestRegressor(n_estimators=1000,  max_features=13 ,max_depth=12, random_state=0)
model.fit(X.to_numpy(),y.to_numpy())
model.score(X.to_numpy(), y.to_numpy())

画图 

sorted_index = model.feature_importances_.argsort()[::-1]
plt.figure(figsize=(10, 8),dpi=128) # 可以调整尺寸以适应所有特征

# 使用 seaborn 来绘制条形图
sns.barplot(x=model.feature_importances_[sorted_index], y=X.columns[sorted_index], orient='h')
plt.xlabel('Feature Importance')  # x轴标签
plt.ylabel('Feature')             # y轴标签
plt.show()

可以看到前面很多变量的贡献程度比较高，后面那些很多变量都没有啥用，所以我们截一下尾，免得图不太好看。

只选前15个画图

sorted_index = model.feature_importances_.argsort()[::-1][:15]
plt.figure(figsize=(10, 8),dpi=128) # 可以调整尺寸以适应所有特征

# 使用 seaborn 来绘制条形图
sns.barplot(x=model.feature_importances_[sorted_index][:15], y=X.columns[sorted_index][:15], orient='h')
plt.xlabel('Feature Importance')  # x轴标签
plt.ylabel('')             # y轴标签
plt.show()

这样我们就能清楚的看到影响汽车价格的是哪些变量了，排名第一的是汽车的引擎容量大小，这个应该代表汽车的性能。排名第二的是汽车的年龄，第三的是它出厂的年限，这两个是一样的。后面还有变量车的类型是不是SUV，可能SUV的价格会高一点，诸如此类.......

模型保存

import joblib
model_filename = 'regressor_model.pkl'
joblib.dump(model, model_filename)
print(f"Model saved to {model_filename}")

这样我们的模型就保存到本地了，下次就不用重新训练，可以直接使用了。

但是由于我们上面做了一些特征工程，所以说原始数据是不方便放进去的，我们得按照上面的特征工程的流程再去把我们的模型进行预测。可能就得自己写个处理脚本才能实现放入几个出来一个y的一个效果。

界面展望

既然本文说是要做一个系统，那么只是做出模型来肯定还是不够的，得做具体应用。我最近发现有一个Streamlit这个包特别好用。它可以把我们的模型嵌入到一个网页端里面，就可以把模型做成一个web可视化开发，然后我们只需要拖动滑块儿输入数值就可以得到预测结果，当然这个应用目前我还没有完成，后面持续更新会把这个应用尝试加上去。感兴趣的擅长做网页开发的同学可以自己先研究使用一下这个包试试。

之后就相当于是一个可应用的程序，输入几个汽车的特征，就可以预测一下这个汽车的价格。也就是标题所谓的系统了。

 

以前的数据分析案例文章可以参考：python数据分析案例

创作不易，看官觉得写得还不错的话点个关注和赞吧，本人会持续更新python数据分析领域的代码文章~

# python # 数据分析 # 机器学习 # 数据挖掘 # pandas # sklearn
Logo
永洪科技数据分析社区

更多推荐

cover

K-means聚类算法原理及python实现

avatar 永洪科技数据分析社区

K-Means（K-均值）聚类算法

聚类，简单来说，就是将一个庞杂数据集中具有相似特征的数据自动归类到一起，称为一个簇，簇内的对象越相似，聚类的效果越好。而在你聚类之前，你对你的目标是未知的，同样以动物为例，对于一个动物集来说，你并不清楚这个数据集内部有多少种类的动物，你能做的只是利用聚类方法将它自动按照特征分为多类，然后人为给出这个聚类结果的定义（即簇识别）。为了更好的了解自己的用户，产品部门可以采用聚类的方法得到不同特征的用户群

avatar 永洪科技数据分析社区

jdk没有jre的解决方法

jdk11以上没有jre的解决方法 小白篇安装的jdk没有jre(JDK11以上版本)解决方法方法一：步骤1：步骤2：注意:方法二：步骤：安装的jdk没有jre(JDK11以上版本)我猜你安装后的jdk目录大概是这样的可以看到，现在的jdk目录下是没有jre的解决方法方法一：步骤1：首先，也是最重要的一步：以管理员身份运行cmd操作方法：在Windows系统的开始菜单上，单击鼠标右键，这时候出现的

avatar 永洪科技数据分析社区