这篇来说说支持向量机，说实在的，这个是我的最爱，一直比较看好这个算法，而且也是花了不少时间在这个上面，下面一起来复习下。同上篇，下面摘自本人的毕业设计论文中，后面给出参考文献。

           基于统计学习理论的支持向量机算法是现代智能技术中的重要方面，研究从观测数据（样本）出发寻找规律，利用这些规律对未来数据或无法观测的数据进行预测。与传统统计学相比，统计学习理论（Statistical Learning Theory，SLT）是一种专门研究小样本情况下机器学习规律的理论。该理论针对小样本统计问题建立了一套新的理论体系，在这种体系下的统计推理规则不仅考虑了对渐近性能的要求，而且追求在现有有限信息的条件下得到最优结果。V. Vapnik等人从六、七十年代开始致力于此方面研究^[36.37]，到九十年代中期，随着其理论的不断发展和成熟，也由于人工神经网络等学习方法在理论上取得实质性进展，统计学习理论开始受到越来越广泛的重视。统计学习理论的一个核心概念就是VC维(Vapnik和Chervonenkis Dimension)概念，它是描述函数集或学习机器的复杂性或者说是学习能力的一个重要指标，在此概念基础上发展出了一系列关于统计学习的一致性、收敛速度、推广性能等的重要结论。统计学习理论是建立在一套较坚实的理论基础之上的，为解决有限样本学习问题提供了一个统一的框架。它能将很多现有方法纳入其中，有望帮助解决许多原来难以解决的问题（比如神经网络结构选择问题、局部极小点问题等）；同时，这一理论基础上发展了一种新的通用学习方法──支持向量机，已初步表现出很多优于已有方法的性能。一些学者认为，SLT和SVM正在成为继ANN研究之后新的研究热点，并将推动机器学习理论和技术有重大的发展^[40]。支持向量机方法是建立在统计学习理论的VC维理论和结构风险最小原理基础上的，根据有限的样本信息在模型的复杂性(即对特定训练样本的学习精度)和学习能力(即无错误地识别任意样本的能力)之间寻求最佳折衷，以期获得最好的推广能力。

       支持向量机方法的几个主要优点有： 1 它是专门针对有限样本情况的，其目标是得到现有信息下的最优解而不仅仅是样本数趋于无穷大时的最优值； 2 算法最终将转化成为一个二次型寻优问题，从理论上说，得到的将是全局最优点，解决了在人工神经网络方法中无法避免的局部极值问题； 3 算法将实际问题通过非线性变换转换到高维的特征空间，在高维空间中构造线性判别函数来实现原空间中的非线性判别函数，特殊性质能保证机器有较好的推广能力，同时它巧妙地解决了维数问题，其算法复杂度与样本维数无关；在SVM方法中，只要定义不同的内积函数，就可以实现多项式逼近、贝叶斯分类器、径向基函数(Radial Basic Function，RBF)方法、多层感知器网络等许多现有学习算法。这使得SVM方法得到了广泛的重视，很多学者进行了积极的探索，做了许多工作^[41-49]。

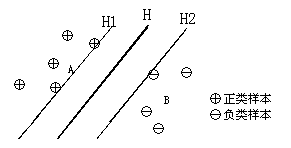
      SVM是从线性可分情况下的最优分类面发展而来的，基本思想可用图2.4的两维情况说明^[38-39]。图中，H为分类线，H1、H2分别为过各类中离分类线最近的样本且平行于分类线的直线，它们之间的距离叫做分类间隔（margin）。所谓最优分类线就是要求分类线不但能将两类正确分开（训练错误率为0），而且使分类间隔最大。

这一特点提供了解决算法可能导致的“维数灾难”问题的方法：在构造判别函数时，不是对输入空间的样本作非线性变换，然后在特征空间中求解；而是先在输入空间比较向量(例如求点积或某种距离)，对结果再作非线性变换。这样，大的工作量将在输入空间而不是在高维特征空间中完成。SVM分类函数形式上类似于一个BPN，输出是中间节点的线性组合，每个中间节点对应一个支持向量，如图2.5所示。函数K称为点积的卷积核函数，它可以看作在样本之间定义的一种距离^[50]。 

参考文献

[40] http://www.suport-vector.net

[41] Platt, J. Fast training of support vector machines using sequential minimal optimization， Advances in Kernel Methods-Support Vector Learning，Cambridge, MA: MIT Press, 1999，185-208.

[42] Keerthi, S.S., Shevade, S.K., Bhattacharyya, Improvements to Platt’s SMO algorithm for SVM classifier design， Technical Report. Bangalore, India: Department of CSA, IISc, 1999

[43] Chang, C.C, Hsu, C.W, Lin, C.J .The analysis of decomposition methods for support vector machines. In: Dean, T., ed. Proceedings of the 16th International Joint Conference on Artificial Intelligence, 1999，25，200-204

[44] YANG Xiaowei,LIN Daying,HAO Zhifeng,LIANG Yanchun,LIU Guirong  and HAN Xu，A fast SVM training algorithm based on the set segmentation and k-means clustering，Progress In Natural Science, 2003.10，13 (10),750-755

[45] ZHU Yongsheng,ZHANG Youyun ,A new type SVM-projected SVM ,Science in China Ser.G Physics & Astronomy ,2004,47,21-27

[46] Kuan-Ming Lin， Chih-Jen Lin， A study on reduced support vector machines Neural Networks, IEEE Transactions , 2003.11,14( 6)

[47] 李红莲,王春花,袁保宗.一种改进的支持向量机NN-SVM.计算机学报,2003 .8, 26(8),1015-1020

[48] 张健沛,徐华. 支持向量机(SVM)主动学习方法研究与应用, 计算机应用第24卷第1期,2004.1,24(1),1-3

[49] 萧嵘,王继成,孙正兴,张福炎, 一种SVM 增量学习算法α- ISVM,软件学报， 2000.7, 12(12),1817-1824