家庭用电居民生活中不可缺少的部分，随着家用电器等设备增多，用电安全已经成为人们最为关心的部分，在用电过程中若出现超负荷的用电，会损坏电器，甚至会造成火灾等事故的发生。另外受利益驱动，出现偷电等现象，传统的检测方式基于人工判断用户电情况进行分析异常，电力工作人员工作压力大，切容易出现漏判误判现象。基于此，通过机器学习知识，挖掘家庭日常用电数据进行分析和异常检测很有必要。本文通过收集用户家庭用电每1分钟数据，对其进行预处理和可视化分析，掌握不同时段不同用途的用电数据，以历史用电数据为样本，构建基于GaussianNB算法的用电数据异常检测模型，通过训练的模型对家庭用电数据的进行异常检测，其检测结果为家庭安全用电和电力工作人员用电异常检测工作提供重要帮助。

选题背景

近年来，随着社会的发展，各种电器化设备逐年增多，根据相关文献[1]可知，我国各界的用电量不断的增加，在一定的利益驱动下，社会上出现了偷电、走电等异常用电个人行为，这种异常用电行为严重的干扰我国供电系统秩序[2],同样也严重危害了电力企业的经济利益。尽管电力企业采用先进的计算机技术来管理电力的使用工作，但是这种管理方式依旧非常落后。目前我国电力行业对窃电、走电等个人行为的检测的主要手段是通过电能计量系统[3]中数据，结合异常报案设备和辅助的电子计算机查询工具来完成对用户用电情况进行检测，并结合电流量过负荷、过压失流[4]等情况来识别用户是否存在异常用电行为，这种传统的检测模式存在的主要问题是出现误判或者漏判情况，没有办法精准判断用户是否存在用电异常情况。随着大数据技术的发展，将挖掘技术和机器学习算法应用在用户用电异常行为检测上，对电力企业和用户都有着重要的现实意义。

选题意义

随着我国社会经济的高速发展，人们生活水平也得到的提高，电力作为人们生活中最为基本的保障条件，它是促进社会发展的重要因素。随着人们用电数量的增多，用电方面的工作压力越来越大，传统的人工检测异常用电情况已经无法满足电力企业发展的需要，因此基于监督学习算法构建用电异常检测模型，对用户用电异常行为自动化检测，能够精确的研判用户是否存在用电异常行为，同时提高电力行业的服务质量，避免用电异常行为的误判情况发生，同时减少电力企业的经济损失。。

国内外研究现状

国内关于用户用电异常检测方面的研究较多，根据知网等可知，许多学者专家对该方面的内容作了研究。2019年，树童[5]就衡水供电公司异常用电大数据进行了研究，并设计了响应的异常用电检测系统，为衡水供电公司异常用电检测工作进行服务。2021年，黄莉雅,倪凡,舒彧[6]等人将用户用电异常检测课题作为研究内容，通过分析研究得窃漏电的相关评价指标，得到其影响因素，通过边缘计算网络模型和神经网络模型来构建异常用电的分类器，通过实验数据验证得到模型准确率，最终他们通过分析通过上述两种模型结合得到的异常用电识别模型准确率高，实用性强。2022年，张丽娟,保富[7]等人基于SVM方法实现异常用电识别，对用户用电数据进行归一化等处理后作为模型训练样本，最后构建一个准确率较高的异常用电识别模型。国外，同样对异常用电方面的检测研究格外重视。2022年，MoureGarrido Marta,Campo Celeste[8]等人基于熵的家庭用电异常检测进行研究和分析。dos Angelos, E.W.S.[9]等人就配电系统中客户用电异常的检测与识别功能进行实现。

朴素贝叶斯算法介绍

朴素贝叶斯算法概述

朴素贝叶斯算法[10]是遵守贝叶斯定理且和特征条件独立假设的分类算法[11]，它的名字中的朴素是指特征条件独立，的名字中的贝叶斯则是指它是基于贝叶斯定理。本算法则是监督学习模型算法，它使用起来十分简单，而且有贝叶斯定理的数据知识作为其坚强的后盾支持，它比较适合大量样本的模型预测。它不适合一些有关联情况的特征条件的样本预测。

朴素贝叶斯的算法原理介绍

朴素贝叶斯的算法是遵守贝叶斯定理，先对贝叶斯定理的相关概念进行介绍。

(1)条件概率[12]，一般是指一个事件A在其他一个事件B已经发生的情况下该事件A的发生概率，通常使用P(A|B)表示当B事件发生是A事件发生的概率。

(2)联合概率，一般是指一个事件A与其他一个事件B一起发生的概率，通常使用P(AB)表示事件A和事件B发生的联合概率。其中事件A和事件B的联合概率公式如下:

当事件A和事件B他们之间是相互独立的情况下，则其中事件A和事件B的联合概率公式如下:

贝叶斯定理[13]，通常一个事件A在其他一个事件B已经发生的情况下该事件A的发生概率与一个事件B在其他一个事件A已经发生的情况下该事件B的发生概率是不一样的，但是他们之间确有关系，这种关系被称之为贝叶斯定理。其公式如下。

朴素贝叶斯方法根据上文的概念可知，它是遵守贝叶斯定理且和特征条件独立假设的分类算法，因此将设定好的训练集，需要根据特征条件独立假设的的规则进行学习输入/输出的联合概率分布，对于输入的数据，通过贝叶斯定理进行求解后验概率对应的最大值y。因此朴素贝叶斯的算法原理实质上是通过设定的输入x,利用学习好的模型进行求解后验概率分布，将求解得到的后验概率中最大的类当作x的类进行输出。得到的朴素贝叶斯分类模型的公式[14]如下所示。

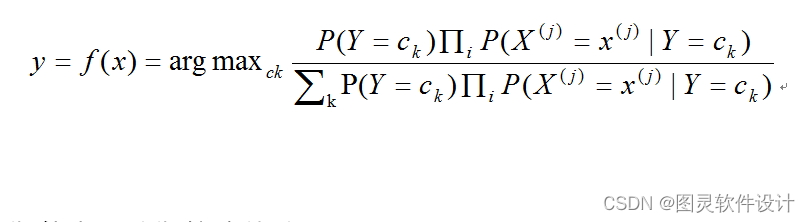
高斯朴素贝叶斯算法基础

高斯朴素贝叶斯算法概述

高斯贝叶斯算法要求设定的样本的对应特征维度的条件概率应该要遵从高斯分布，然后根据上文阐述的贝叶斯公式进行计算这个新样本在某一个特征分布下它对应不同类别的后验概率，得到不同的后验概率值后，采用极大化后验概率的方法完成样本类别的划分，将这个实现过程叫做高斯贝叶斯算法。

高斯朴素贝叶斯算法原理

高斯朴素贝叶斯算法中，设定的数据样本对应不同类情况下，对于每个特征变量对应的条件概率要求服从高斯分布，每个特征变量对应的条件概率计算公式[15]如(2.5)所示。