先有矩阵，然后有行列式。矩阵常有，而行列式不常有。
矩阵是存储数据的，单独的一个数，从本质来讲，也是矩阵，不过是1行1列的。行列式的意义在于发现矩阵中数据的特征。
矩阵存储数据，因而，如果加以某种运算，矩阵是可以作用到其他矩阵上的，并且可以改变原矩阵。例如，2、5同是1行1列矩阵，2*5=10，矩阵2，通过矩阵5的作用，变成了矩阵10。将这种性质扩展到多维空间中，便是矩阵变化，也就是说，矩阵也可以理解为某种变换。矩阵既可以代表坐标，也可以代表变化，至于怎么样理解矩阵最到位（有些同学喜欢研究矩阵的本质，其实矩阵的本质诚如刚才的例子，就是存储数据的。不要纠结于一定要感知到矩阵的本质。），就看具体的情形了。
矩阵从1维到2维的过程中，会存在某些性质的变化，而从2维再到更高维，这种变化可以类推（可类比微积分中的微分和导数），故而，在矩阵的研究过程中，二次型是重要的一个环节。
按照惯例，在矩阵变换两个相乘的矩阵中，位于左边的矩阵，我们认为是变换，位于右边的矩阵，认为是原矩阵。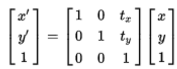

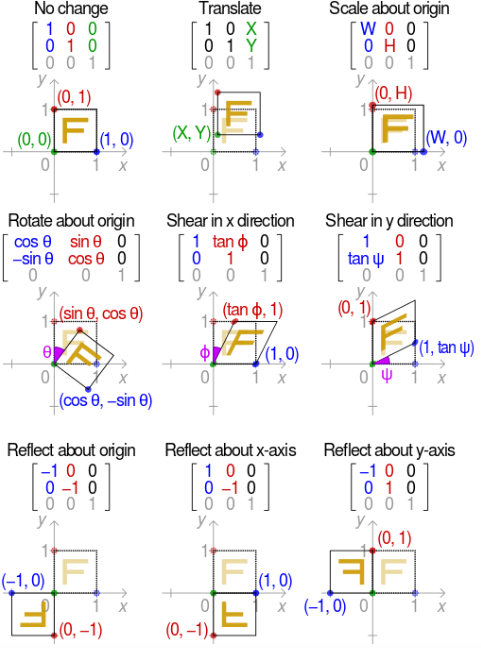
[x,y,1]’ 代表原矩阵，在不同的变化下，原矩阵（此例中即为三维空间中的点）可发生下面的变换：