转载请注明出处,内容引用和感谢部分将会在文章末尾一并给出!
1.关联规则浅谈
关联规则(Association Rules)是反映一个事物与其他事物之间的相互依存性和关联性,如果两个或多个事物之间存在一定的关联关系,那么,其中一个事物就能通过其他事物预测到。关联规则是数据挖掘的一个重要技术,用于从大量数据中挖掘出有价值的数据项之间的相关关系。
关联规则首先被Agrawal, lmielinski and Swami在1993年的SIGMOD会议上提出。
关联规则挖掘的最经典的例子就是沃尔玛的啤酒与尿布的故事,通过对超市购物篮数据进行分析,即顾客放入购物篮中不同商品之间的关系来分析顾客的购物习惯,发现美国妇女们经常会叮嘱丈夫下班后为孩子买尿布,30%-40%的丈夫同时会顺便购买喜爱的啤酒,超市就把尿布和啤酒放在一起销售增加销售额。有了这个发现后,超市调整了货架的设置,把尿布和啤酒摆放在一起销售,从而大大增加了销售额。
2.常见案例
前面讲述了关联规则挖掘对超市购物篮的例子,使用Apriori对数据进行频繁项集挖掘与关联规则的产生是一个非常有用的技术,其中我们众所周知的例子如:
(1) 沃尔玛超市的尿布与啤酒
(2) 超市的牛奶与面包
(3) 百度文库推荐相关文档
(4) 淘宝推荐相关书籍
(5) 医疗推荐可能的治疗组合
(6) 银行推荐相关联业务
这些都是商务智能和关联规则在实际生活中的运用
3.关联规则的3个度量
支持度(support):说明规则的统计显著性

置信度(confidence):说明规则的强度(最小和最大置信度有公司设定)

还有其他的度量标准,比如:提升度/兴趣度(interest),但是前面提出的这两个较为常用!
4. Apriori算法简介
我们的目标是找出具有足够高的支持度和置信度的所有规则,并且由于销售数据库一般非常大,所有我们希望通过少数几遍数据库扫描就找出它们。所以这里就提出了一个有效算法,称为Apriori算法(Agrawal等1996)来做这项工作。Apriori算法是一种对有影响的挖掘布尔关联规则频繁项集的算法,通过算法的连接和剪枝即可挖掘频繁项集。
该算法分为两步:
(1)找出频繁项集,即找出具有足够支持度的项集;
这里补充 频繁项集的概念:
频繁项集:如果项集的出现频率大于或等于最小支持度计数阈值,则称它为频繁项集,其中频繁K-项集的集合通常记作Lk
下图详细描述了找出频繁项集的过程:
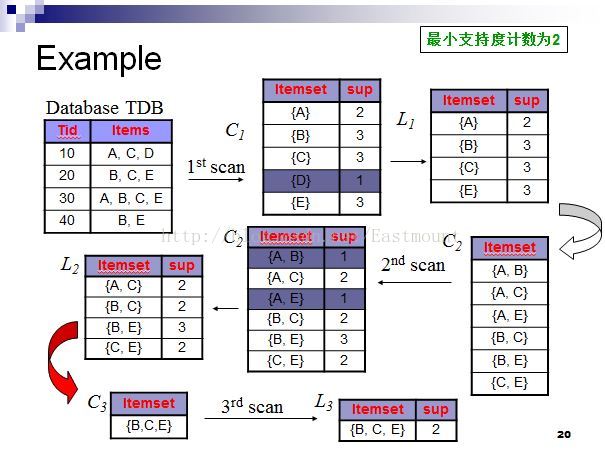
具体分析结果:
第一次扫描:对每个候选商品计数得C1,由于候选{D}支持度计数为1<最小支持度计数2,故删除{D}得频繁1-项集合L1;
第二次扫描:由L1产生候选C2并对候选计数得C2,比较候选支持度计数与最小支持度计数2得频繁2-项集合L2;
第三次扫描:用Apriori算法对L2进行连接和剪枝产生候选3项集合C3的过程如下:
1.连接:
C3=L2(连接)L2={{A,C},{B,C},{B,E},{C,E}}{{A,C},{B,C},{B,E},{C,E}}={{A,B,C},{A,C,E},{B,C,E}}
2.剪枝:
{A,B,C}的2项子集{A,B},{A,C}和{B,C},其中{A,B}不是2项子集L2,因此不是频繁的,从C3中删除;
{A,C,E}的2项子集{A,C},{A,E}和{C,E},其中{A,E}不是2项子集L2,因此不是频繁的,从C3中删除;
{B,C,E}的2项子集{B,C},{B,E}和{C,E},它的所有2项子集都是L2的元素,保留C3中。
经过Apriori算法对L2连接和剪枝后产生候选3项集的集合为C3={B,C,E}. 在对该候选商品计数,由于等于最小支持度计数2,故得频繁3-项集合L3,同时由于4-项集中仅1个,故C4为空集,算法终止。
(2)通过把频繁项集划分成两个子集,分别作为前件和后件,把频繁项集转换成具有足够置信度的规则;
强关联规:如果规则R:X=>Y满足support(X=>Y)>=supmin(最小支持度,它用于衡量规则需要满足的最低重要性)且confidence(X=>Y)>=confmin(最小置信度,它表示关联规则需要满足的最低可靠性)称关联规则X=>Y为强关联规则,否则称关联规则X=>Y为弱关联规则。
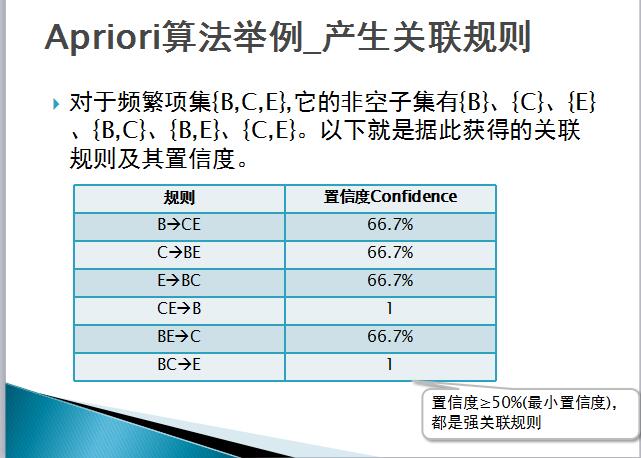
例子:现有A、B、C、D、E五种商品的交易记录表,找出所有频繁项集,假设最小支持度>=50%,最小置信度>=50%。
对于关联规则R:A=>B,则:
支持度(suppport):是交易集中同时包含A和B的交易数与所有交易数之比。
Support(A=>B)=P(A∪B)=count(A∪B)/|D|
置信度(confidence):是包含A和B交易数与包含A的交易数之比。
Confidence(A=>B)=P(B|A)=support(A∪B)/support(A)
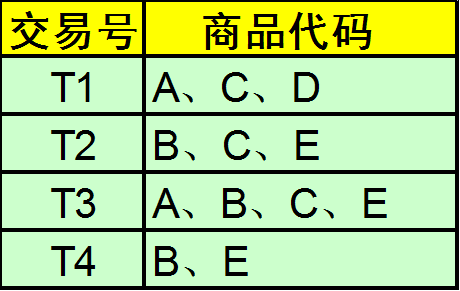
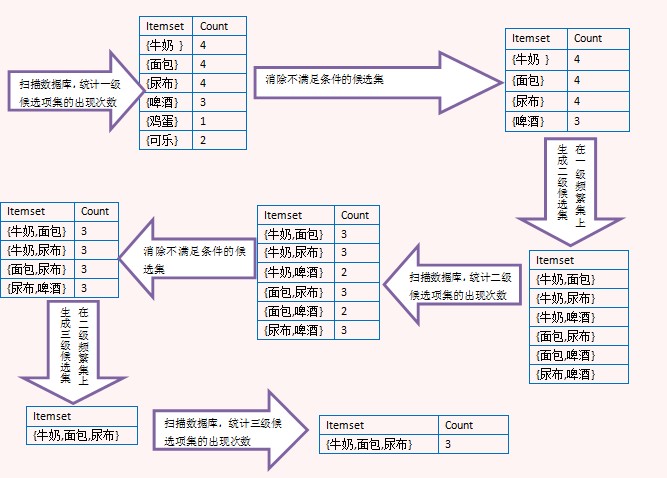
计算过程如下,K=1的时候项集{A}在T1、T3中出现2次,共4条交易,故支持度为2/4=50%,依次计算。其中项集{D}在T1出现,其支持度为1/4=25%,小于最小支持度50%,故去除,得到L1。
然后对L1中项集两两组合,再分别计算其支持度,其中项集{A, B}在T3中出现1次,其支持度=1/4=25%,小于最小支持度50%,故去除,同理得到L2项集。
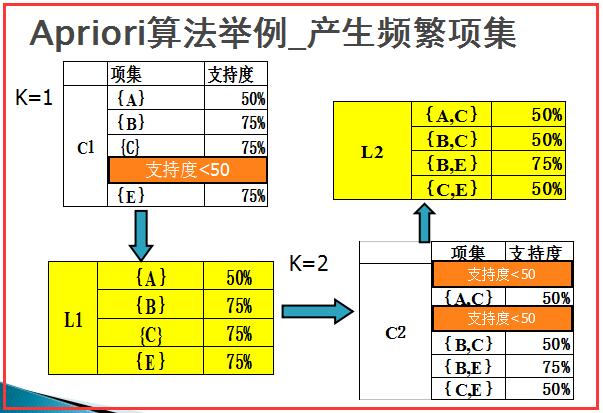
然后如下图所示,对L2中的项集进行组合,其中超过三项的进行过滤,最后计算得到L3项集{B,C,E}。
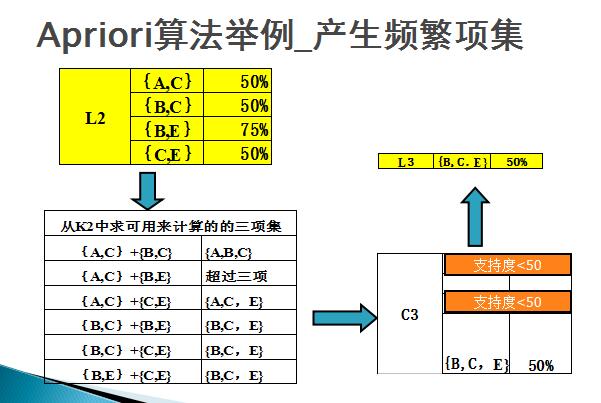
最后对计算置信度,如下图所示。
Apriori算法弊端:需要多次扫描数据表。如果频繁集最多包含10个项,那么就需要扫描交易数据表10遍,这需要很大的I/O负载。同时,产生大量频繁集,若有100个项目,可能产生候选项数目。
![]()
故:Jiawei Han等人在2000年提出了一种基于FP-树的关联规则挖掘算法FP_growth,它采取“分而治之”的策略,将提供频繁项目集的数据库压缩成一棵频繁模式树(FP-树)。
推荐一张图,详细分析关联规则的过程:
原文作者参考文献:
[1]高明 . 关联规则挖掘算法的研究及其应用[D].山东师范大学. 2006
[2]李彦伟 . 基于关联规则的数据挖掘方法研究[D].江南大学. 2011
[3]肖劲橙,林子禹,毛超.关联规则在零售商业的应用[J].计算机工程.2004,30(3):189-190.
[4]秦亮曦,史忠植.关联规则研究综述[J].广西大学学报.2005,30(4):310-317.
[5]陈志泊,韩慧,王建新,孙俏,聂耿青.数据仓库与数据挖掘[M].北京:清华大学出版社.2009.
[6]沈良忠.关联规则中Apriori 算法的C#实现研究[J].电脑知识与技术.2009,5(13):3501-3504.
[7]赵卫东.商务智能(第二版)[M].北京:清华大学出版社.2011.
5. Apriori算法代码实现(暂时使用引用地址处的代码,后期会更新个人书写代码)
# -*- coding: utf-8 -*-
"""
Created on Mon Nov 28 03:29:51 2016
地址:http://blog.csdn.net/u010454729/article/details/49078505
@author: 参考CSDN u010454729
"""
# coding=utf-8
def loadDataSet():
return [[1,3,4],[2,3,5],[1,2,3,5],[2,5]]
def createC1(dataSet): #构建所有候选项集的集合
C1 = []
for transaction in dataSet:
for item in transaction:
if not [item] in C1:
C1.append([item]) #C1添加的是列表,对于每一项进行添加,{1},{3},{4},{2},{5}
C1.sort()
return map(frozenset, C1) #使用frozenset,被“冰冻”的集合,为后续建立字典key-value使用。
def scanD(D,Ck,minSupport): #由候选项集生成符合最小支持度的项集L。参数分别为数据集、候选项集列表,最小支持度
ssCnt = {}
for tid in D: #对于数据集里的每一条记录
for can in Ck: #每个候选项集can
if can.issubset(tid): #若是候选集can是作为记录的子集,那么其值+1,对其计数
if not ssCnt.has_key(can):#ssCnt[can] = ssCnt.get(can,0)+1一句可破,没有的时候为0,加上1,有的时候用get取出,加1
ssCnt[can] = 1
else:
ssCnt[can] +=1
numItems = float(len(D))
retList = []
supportData = {}
for key in ssCnt:
support = ssCnt[key]/numItems #除以总的记录条数,即为其支持度
if support >= minSupport:
retList.insert(0,key) #超过最小支持度的项集,将其记录下来。
supportData[key] = support
return retList, supportData
def aprioriGen(Lk, k): #创建符合置信度的项集Ck,
retList = []
lenLk = len(Lk)
for i in range(lenLk):
for j in range(i+1, lenLk): #k=3时,[:k-2]即取[0],对{0,1},{0,2},{1,2}这三个项集来说,L1=0,L2=0,将其合并得{0,1,2},当L1=0,L2=1不添加,
L1 = list(Lk[i])[:k-2]
L2 = list(Lk[j])[:k-2]
L1.sort()
L2.sort()
if L1==L2:
retList.append(Lk[i]|Lk[j])
return retList
def apriori(dataSet, minSupport = 0.5):
C1 = createC1(dataSet)
D = map(set,dataSet)
L1, supportData = scanD(D,C1,minSupport)
L = [L1] #L将包含满足最小支持度,即经过筛选的所有频繁n项集,这里添加频繁1项集
k = 2
while (len(L[k-2])>0): #k=2开始,由频繁1项集生成频繁2项集,直到下一个打的项集为空
Ck = aprioriGen(L[k-2], k)
Lk, supK = scanD(D, Ck, minSupport)
supportData.update(supK) #supportData为字典,存放每个项集的支持度,并以更新的方式加入新的supK
L.append(Lk)
k +=1
return L,supportData
dataSet = loadDataSet()
C1 = createC1(dataSet)
print "所有候选1项集C1:\n",C1
D = map(set, dataSet)
print "数据集D:\n",D
L1, supportData0 = scanD(D,C1, 0.5)
print "符合最小支持度的频繁1项集L1:\n",L1
L, suppData = apriori(dataSet)
print "所有符合最小支持度的项集L:\n",L
print "频繁2项集:\n",aprioriGen(L[0],2)
L, suppData = apriori(dataSet, minSupport=0.7)
print "所有符合最小支持度为0.7的项集L:\n",L
运行结果:
所有候选1项集C1:
[frozenset([1]), frozenset([2]), frozenset([3]), frozenset([4]), frozenset([5])]
数据集D:
[set([1, 3, 4]), set([2, 3, 5]), set([1, 2, 3, 5]), set([2, 5])]
符合最小支持度的频繁1项集L1:
[frozenset([1]), frozenset([3]), frozenset([2]), frozenset([5])]
所有符合最小支持度的项集L:
[[frozenset([1]), frozenset([3]), frozenset([2]), frozenset([5])], [frozenset([1, 3]), frozenset([2, 5]),
frozenset([2, 3]), frozenset([3, 5])], [frozenset([2, 3, 5])], []]
频繁2项集:
[frozenset([1, 3]), frozenset([1, 2]), frozenset([1, 5]), frozenset([2, 3]), frozenset([3, 5]), frozenset([2, 5])]
所有符合最小支持度为0.7的项集L:
[[frozenset([3]), frozenset([2]), frozenset([5])], [frozenset([2, 5])], []]
引文及参考:
1.本文主要参考地址:https://blog.csdn.net/Eastmount/article/details/53368440
2.本文参考图书《机器学习导论》
代码后续会及时补充完善,如需转载,请尊重作者的辛勤付出,注明文章来源!
记录生活,分享技术!










 已为社区贡献432条内容
已为社区贡献432条内容

所有评论(0)