首先必须要声明一下，我不是专业做贝叶斯的，写这篇文章主要是科普，其中涉及到的数学公式我会用更加浅显易懂的方式来描述，方便大家都能够有所收获。同时我认为贝叶斯并不是机器学习的专属，了解一下这个神级算法，打开一扇窗，相信你会有不同的看法。

源头

聊一个算法就要清楚它的历史，它怎么来的，最先用来解决什么实际问题，它根本原理以及推导过程是怎么样的，在现在有什么重要的应用，以及对于未来贝叶斯发展有什么看法等，这既是一套了解一个算法的流程，也是一种分析问题的思路。

先聊一聊贝叶斯算法是怎么来的，看一下维基百科上面的描述

所谓的贝叶斯方法源于贝叶斯生前为解决一个“逆概”问题写的一篇文章，而这篇文章是在他死后才由他的一位朋友发表出来的。在贝叶斯写这篇文章之前，人们已经能够计算“正向概率”，如“假设袋子里面有N个白球，M个黑球，你伸手进去摸一把，摸出黑球的概率是多大”。而一个自然而然的问题是反过来：“如果我们事先并不知道袋子里面黑白球的比例，而是闭着眼睛摸出一个（或好几个）球，观察这些取出来的球的颜色之后，那么我们可以就此对袋子里面的黑白球的比例作出什么样的推测”。这个问题，就是所谓的逆概问题。

这么说就比较抽象，我们用一个实际生活的例子来详解贝叶斯，顺便体会它的应用。

算命问题

首先需要普及两个概念，先验概率和后验概率，不明白？上例子。

村里面以前会有一些算命先生，测吉凶，但是作为算命先生来讲如何测的更加准确甚至是百发百中呢。算命先生通常会通过问一些问题来达到他对于你的了解。今天假设小布是算命先生，现在开始算命了，如果我对这个人没有任何了解，包括他的年龄、居住环境等等。按统计学的角度来说，一个人有三高（高血压、高血脂、高血糖）的概率咱们先认为是20%。那么，这个概率 P(三高) 就被称为先验概率。

什么是先验概率呢？也就是根据以往经验和分析得到的概率，这是一个大数据统计下基本是可信的数据。先验概率不受任何条件的影响，也不用我们用数据验证，在一定时间内基本不会发生变化。

再来看，小布了解到如果一个人大于70岁没有三高的可能性就比较小。年龄大之后很多病都伴随着来了，70岁后有三高的概率就比年轻的时候大一些，我们先计做是60%。如果把年龄大于70当作一种结果，然后去推测这个人活到是否有三高的概率，在这里我们把>70这个事件记作>70，没有三高这个事件计为没三高，这个概率 P(没三高 | >70) 就被称为后验概率。P(A|B)

再说，当知道了先验概率和后验概率，我们再来看看什么是联合概率。算命的例子中，P(没三高,70) 称之为联合分布，它表示活到70岁了且没有三高的概率。关于联合概率，满足下列乘法等式：

其中，P(没三高|>70) 就是刚刚介绍的后验概率，表示在“大于70岁”的条件下，“没有三高”的概率。P(70 | 没三高) 表示在“没三高”的情况下，一个人“大于70岁”的概率。

接着，小布想如何计算一个人没有三高的概率呢？当然我们可以根据年龄讲没有三高的概率分成两种情况：一种是年龄大于70且有三高的情况，另一种是年龄小于70且有三高的情况。一个人没有三高的概率就是这两种情况之和。因此，我们就推导出了全概率公式：

P(没有三高）=P(没有三高,>70)+P(没有三高,<70)=P(没有三高|>70).P(>70)+P(没有三高|<70).P(<70)

单个特征判断三高

好了，介绍完先验概率、后验概率、联合概率、全概率后，我们来看这样一个问题：三高的状态分成两种：没三高与有三高，概率分别为 0.8与0.2，且没三高的人群里面大于70岁的概率是0.2，有三高里面大于70岁的概率是0.7。那么，如果我遇到一个大于70的人，这个人没有三高的概率多大？

显然，这是一个计算后验概率的问题，根据我们上面推导的联合概率和全概率公式，可以求出：

一项一项来看：

条件概率 P(>70 | 没三高) = 0.2，
先验概率 P(没三高) = 0.8，
条件概率 P(>70 | 三高) = 0.7，先验概率 P(三高) = 0.2

将以上数值带入上式，得：

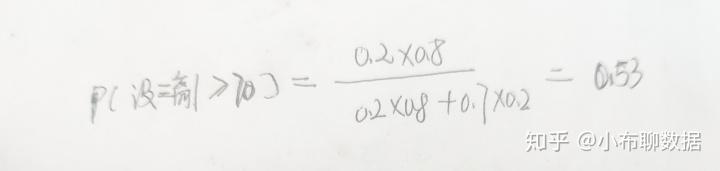
这样，我们就计算得到了大于70岁有三高的概率是 0.53。注意，以上这种计算后验概率的公式就是利用贝叶斯定理。有点意外吧？不知不觉，可以说你已经掌握了贝叶斯定理的思想了。

多个特征判断是否三高

为了确定这个人是不是三高，需要更多的因素。除了要看年龄是不是比较大，还要看体型和性别。体型有胖和瘦之分，性别分男女。这么多特征我们怎么利用起来呢？可以使用刚刚引入的贝叶斯定理思想来尝试解决这个问题。

现在，特征由原来的 1 个，变成现在的 3 个，我们用 X 表示特征，用 Y 表示是否三高。则根据贝叶斯定理，后验概率 P(Y=ck | X=x) 的表达式为：

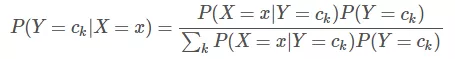
其中，ck 表示类别，k 为类别个数。本例中，k = 1，2，c1 表示有三高，c2 表示没有三高。上面的公式看似有点复杂，但其实与单特征（年龄是否大于70）的形式是一致的。

有一点需要注意，这里的特征 X 不再是单一的，而是包含了 3 个特征。因此，条件概率 P(X=x | Y=ck) 假设各个条件相互独立，也就是说假设不同特征之间是相互独立的。这样，P(X=x | Y=ck) 就可以写成：

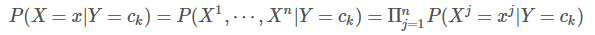
其中，n 为特征个数，j 表示当前所属特征。针对这个例子，P(X=x | Y=ck) 可以写成：

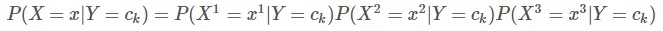
这样看起来可能还是有些别扭，我们把每个里面的Y=ck这个条件隐去，是不是就比较熟悉了。

这种条件独立性的假设就是朴素贝叶斯法“朴素”二字的由来。这一假设让朴素贝叶斯法变得简单，但是有时候会牺牲一定的分类准确率。这样，利用朴素贝叶斯思想，我们就可以把后验概率写成：

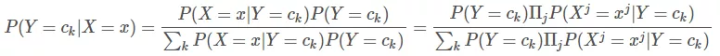
现在，小布算命先生看到一个人，知道了他的性别、体型、年龄三个特征，就能根据上面的朴素贝叶斯公式，分别计算 c1（有三高）和 c2（没三高）的概率，即 P(Y=c1 | X=x) 和 P(Y=c2 | X=x)。然后再比较 P(Y=c1 | X=x) 和 P(Y=c2 | X=x) 值的大小：

若 P(Y=c1 | X=x) > P(Y=c2 | X=x)，即，有三高的概率更大；

若 P(Y=c1 | X=x) < P(Y=c2 | X=x)，即，没三高的概率更大。

值得注意的是上式中的分母部分，对于所有的 ck 来说，都是一样的。因此，分母可以省略，不同的 ck，仅比较 P(Y=ck | X=x) 的分子即可：

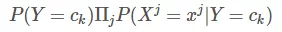
机器学习与朴素贝叶斯

当然我们在做这个的过程中，还是忽略了一些问题，先验概率是怎么得出来的，这也就开始和我们的机器学习挂钩了，需要有一些历史数据让我们知道先验概率，这就是计算机进行学习的基本数据，为了达到一定的准确性，我们常常需要喂给机器大量的数量，让他能够更加准确的计算先验概率，随着根据既定的贝叶斯算法，我们输入一个人的几个特征值，进而就能输出一个结果这个人是不是有三高，这种根据特征值判断的方式就是分类的方式。比如面部识别，首先需要大量的人脸数据来选取能够特定识别的特征值，每一次人脸的记录都是一次学习，都会形成一个类似于特征值表格的东西，对特征值进行分类，不过为了保证准确率，需要的特征值一定是非常多的。根据特征值来判断你是不是张三或者是不是李四。