大数据安全 | 【实验】S-AES加密
S-AES加密。
文章目录
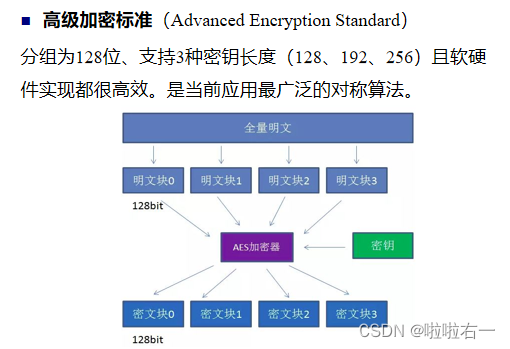
📚关于AES


📚实验目的
- 实现 S-AES加密。
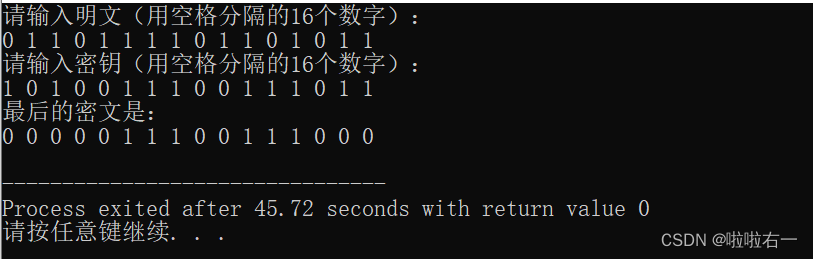
- 测试数据:使用密钥 1010 0111 0011 1011 加密二进制明文 0110 1111 0110 1011,得出二进制密文 0000 0111 0011 1000。
📚流程梳理
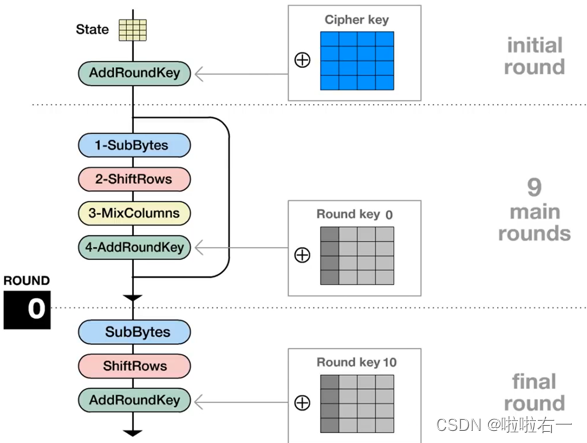
- S-AES 是 AES 加解密方法的缩减版。AES 的明文包括 128 位、256 位等处理,而 S-AES 只是对 16 位二进制明文进行处理;
- AES 需要进行 0+10 轮加密,而S-AES 只进行 0+2 轮加密
- 第0轮只进行
轮密钥加- 第一轮进行
字节替换、行变换、列混淆和轮密钥加- 第二轮只进行
字节替换、行变换和轮密钥加
🐇Step1:密钥扩展算法
-
密钥的左半部分:
key1[0] = OR_8(key[0], g(key[1], rcon1));- g函数:
g(key[1], rcon1)- 将第i-1个密钥的右半部分(8位)进行左循环移位,即将第i-1个密钥的右半部分的左右4位进行交换
- 再将左循环移位后的第i-1个密钥的右半部分(8位)进行字节替换
- 进行字节替换后需要与轮常数进行异或
OR_8(key[0], g(key[1], rcon1))- 将第i-1个密钥的右半部分(8位)执行完g函数后得到
g(第i-1个密钥的右半部分) - 将其与第i-1个密钥的左半部分(8位)进行异或得到第
i个密钥的左半部分。
- 将第i-1个密钥的右半部分(8位)执行完g函数后得到
- g函数:
-
密钥的右半部分:
key1[1] = OR_8(key1[0], key[1]);。第i个密钥的右半部分由第i个密钥的左半部分与第i-1个密钥的右半部分进行异或得到。//密钥扩展算法,需要扩展出两个密钥key1和key2 int **key1 = new int *[2]; for (int i = 0; i < 2; i++) key1[i] = new int[8]; int **key2 = new int *[2]; for (int i = 0; i < 2; i++) key2[i] = new int[8]; //key1生成 key1[0] = OR_8(key[0], g(key[1], rcon1)); key1[1] = OR_8(key1[0], key[1]); //key2生成 key2[0] = OR_8(key1[0], g(key1[1], rcon2)); key2[1] = OR_8(key2[0], key1[1]);
🔥8位的异或
- 对两个8位数组进行异或操作(4位异或也是同理)。
//8位的异或 int *OR_8(int *a, int *b) { int *result = new int[8]; for (int i = 0; i < 8; i++) result[i] = a[i] ^ b[i]; return result; }
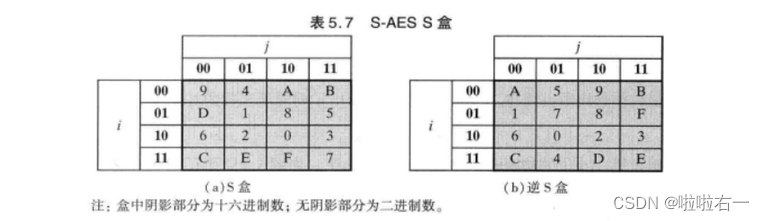
🔥字节替换
-
使用 S 盒进行不同位置的内容的替换。
-
具体而言,对 16 位二进制明文,8 位一组,每组中包含两个 16 进制的二进制表达,也就是 4 位为一个单位进行字节替代。前两位求其十进制得到行号,后两位求其十进制得到列号。
-
然后到 S 盒中找到替换的那几组数据替换上,每次调用函数替换一组,共换 4 个单位的数据。
//字节替换 void SubBytes(int *temp) { //将8位二进制分组为4个2位的数字,这里的×2使得t的范围为0~3,可在表中对应位置检索 int t1 = 2 * temp[0] + temp[1]; int t2 = 2 * temp[2] + temp[3]; int t3 = 2 * temp[4] + temp[5]; int t4 = 2 * temp[6] + temp[7]; //在S盒中找到替换后的值 int num1 = s[t1][t2]; int num2 = s[t3][t4]; //分别进行四位四位的替换 for (int i = 0; i < 4; i++) temp[i] = Replace[num1][i]; for (int i = 0; i < 4; i++) temp[i + 4] = Replace[num2][i]; }
🔥g函数
- 将第i-1个密钥的右半部分(8位)进行左循环移位,即将第i-1个密钥的右半部分的左右4位进行交换
- 再将左循环移位后的第i-1个密钥的右半部分(8位)进行字节替换
- 进行字节替换后需要与轮常数进行异或
//g函数 int *g(int *temp, int *rcon) { //这个temp是密钥的右半部分,不能改动,要复制一个新的进行计算 int *t = new int[8]; for (int i = 0; i < 8; i++) t[i] = temp[i]; //循环左移,即左右4位进行交换 for (int i = 0; i < 4; i++) { int tt = t[i + 4]; t[i + 4] = t[i]; t[i] = tt; } //移位后的右半部分进行字节替换 SubBytes(t); //与轮常数异或 return OR_8(t, rcon); }
🐇Step2:第0轮
- 只进行
轮密钥加,即AddRoundKey(plaintext, key);
🔥轮密钥加
-
轮密钥加就是每组与密钥的每组分别异或。
-
第0轮中使用的是初始密钥
-
第一轮用到的是密钥拓展后的第一个 8 位密钥,即key1
-
第二轮用到的是密钥拓展后的第二个 8 位密钥,即key2
//轮秘钥加 void AddRoundKey(int **mingwen, int **key) { for (int i = 0; i < 2; i++) for (int j = 0; j < 8; j++) mingwen[i][j] ^= key[i][j]; }
🐇Step3:第一轮
- 第一轮进行
字节替换、行变换、列混淆和轮密钥加// 第一轮 // 明文半字节代替 SubBytes(plaintext[0]); SubBytes(plaintext[1]); // 明文的行变换 ShiftRows(plaintext); // 明文的列混淆 MixColumns(plaintext); // 明文的轮密钥加 AddRoundKey(plaintext, key1);
🔥行变换
-
行变换的规则:第一行不变,第二行左移 1 位,依次类推。


关注60是一个字节,4C是一个字节!所以从咱们数组上看,就是第一字节的右半部分和第二字节的右半部分进行替换。
//行变换
void ShiftRows(int **temp)
{
//第一字节的右半部分和第二字节的右半部分进行替换
for(int i = 4;i < 8;i ++)
{
int t = temp[0][i];
temp[0][i] = temp[1][i];
temp[1][i] = t;
}
}
🔥列混淆
-
列混淆本质上就是乘上一个矩阵,运算定义在 G F ( 2 4 ) GF(2^4) GF(24),所以乘上矩阵[[1,4],[4,1]],于是我们可以得出运算公式:
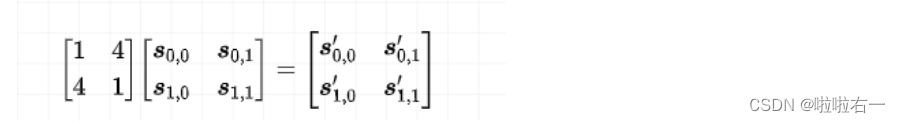
-
其中 S 0 , 0 S_{0,0} S0,0 和 S 1 , 0 S_{1,0} S1,0是一个字节,各为4位。 S 0 , 1 S_{0,1} S0,1 和 S 1 , 1 S_{1,1} S1,1是一个字节,各为4位。得到:
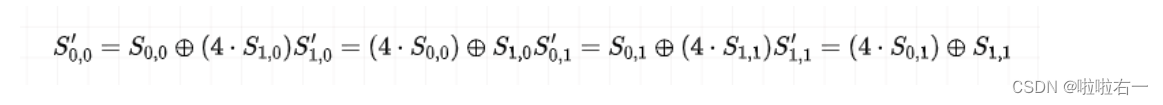
-
“加”实际上是异或。
-
“乘”

-
x_fx函数用于计算 x*f(x),即将多项式 f(x) 进行左移,并根据最高次数是否为 1 进行取模操作(原理类似下图)。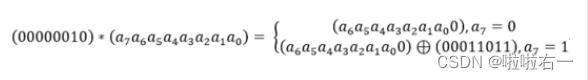
-
multiply函数用于进行多项式乘法操作,在有限域 GF(2^8) 上进行。- 乘法 a(x)*b(x)可以拆成多个 a(x)*x^n 的异或操作。
- 首先根据输入多项式 a,使用
x_fx函数计算 a ∗ ( x 1 ) a*(x^1) a∗(x1)、 a ∗ ( x 2 ) a*(x^2) a∗(x2) 和 a ∗ ( x 3 ) a*(x^3) a∗(x3) 分别得到 x1fx、x2fx 和 x3fx。 - 根据输入多项式 b 的系数,分别使用异或操作符对 x3fx、x2fx、x1fx 和 a 进行运算,得到结果数组 result。
-
MixColumns函数用于进行列混淆操作,输入为明文矩阵 mingwen。-
定义固定的二进制数 rule = {0, 1, 0, 0}(就是4),用于进行乘法计算。
-
将 mingwen 第一行和第二行的元素分别存储到 m00、m10、m01 和 m11 数组中。
-
使用
multiply函数分别计算结果,得到 n00、n10、n01 和 n11。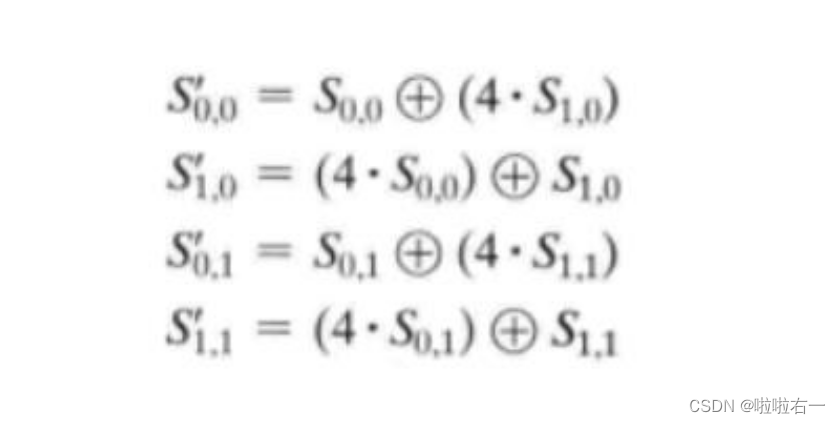
-
更新 mingwen 矩阵,将 n00、n10、n01 和 n11 的元素分别放回 mingwen 中对应的位置。
-
-
最终得到经过列混淆操作后的明文矩阵。
//实现x*f(x)的函数 void x_fx(int last[4], int res[4]) { //res是结果,last是上一步的结果 if (last[0] == 0) { //最高次为0 for (int i = 0; i < 3; i++) //低三项分别升幂次 res[i] = last[i + 1]; } else { //最高次为1 res[1] = last[2]; res[2] = last[3] == 1 ? 0 : 1; res[3] = 1; } } //乘法 int *multiply(int a[4], int b[4]) { //储存结果的系数 int *result = new int[4]; for (int i = 0; i < 4; i++) result[i] = 0; //记录下a*(x^n) int x1fx[4] = {0}; x_fx(a, x1fx);//a*(x^1)=a*{0,0,1,0}=a*b3 int x2fx[4] = {0}; x_fx(x1fx, x2fx);//a*(x^2)=a*{0,1,0,0}=a*b2 int x3fx[4] = {0}; x_fx(x2fx, x3fx);//a*(x^3)=a*{1,0,0,0}=a*b1 //现在需要根据多项式a和b开始异或 if (b[0] == 1)//b1=={1,0,0,0} for (int i = 0; i < 4; i++) result[i] ^= x3fx[i]; if (b[1] == 1)//b2=={0,1,0,0} for (int i = 0; i < 4; i++) result[i] ^= x2fx[i]; if (b[2] == 1)//b3=={0,0,1,0} for (int i = 0; i < 4; i++) result[i] ^= x1fx[i]; if (b[3] == 1)//b4=={0,0,0,1} for (int i = 0; i < 4; i++) result[i] ^= a[i]; return result; } //列混淆 void MixColumns(int **mingwen) { int rule[4] = {0, 1, 0, 0}; int *m00 = new int[4]; // 第一行的前4个元素 int *m10 = new int[4]; // 第一行的后4个元素 int *m01 = new int[4]; // 第二行的前4个元素 int *m11 = new int[4]; // 第二行的后4个元素 for (int i = 0; i < 4; i++) { m00[i] = mingwen[0][i]; m10[i] = mingwen[0][i + 4]; m01[i] = mingwen[1][i]; m11[i] = mingwen[1][i + 4]; } int *n00 = new int[4]; int *n10 = new int[4]; int *n01 = new int[4]; int *n11 = new int[4]; n00 = OR_4(m00, multiply(rule, m10)); n10 = OR_4(multiply(rule, m00), m10); n01 = OR_4(m01, multiply(rule, m11)); n11 = OR_4(multiply(rule, m01), m11); for (int i = 0; i < 4; i++) { mingwen[0][i] = n00[i]; mingwen[0][i + 4] = n10[i]; mingwen[1][i] = n01[i]; mingwen[1][i + 4] = n11[i]; } }
🐇Step4:第二轮
-
第二轮只进行
字节替换、行变换和轮密钥加// 第二轮 // 明文半字节代替 SubBytes(plaintext[0]); SubBytes(plaintext[1]); // 明文的行移位 ShiftRows(plaintext); // 明文的轮密钥加 AddRoundKey(plaintext, key2);
📚实验结果
🐇C++
#include <bits/stdc++.h>
using namespace std;
//S盒
const int s[4][4] = {
{9, 4, 10, 11},
{13, 1, 8, 5},
{6, 2, 0, 3},
{12, 14, 15, 7}};
//替换表
const int Replace[16][4] = {
{0, 0, 0, 0},
{0, 0, 0, 1},
{0, 0, 1, 0},
{0, 0, 1, 1},
{0, 1, 0, 0},
{0, 1, 0, 1},
{0, 1, 1, 0},
{0, 1, 1, 1},
{1, 0, 0, 0},
{1, 0, 0, 1},
{1, 0, 1, 0},
{1, 0, 1, 1},
{1, 1, 0, 0},
{1, 1, 0, 1},
{1, 1, 1, 0},
{1, 1, 1, 1}};
//轮常数
int rcon1[8] = {1, 0, 0, 0, 0, 0, 0, 0};
int rcon2[8] = {0, 0, 1, 1, 0, 0, 0, 0};
//8位的异或
int *OR_8(int *a, int *b)
{
int *result = new int[8];
for (int i = 0; i < 8; i++)
result[i] = a[i] ^ b[i];
return result;
}
//字节替换
void SubBytes(int *temp)
{
//将8位二进制分组为4个2位的数字
int t1 = 2 * temp[0] + temp[1];
int t2 = 2 * temp[2] + temp[3];
int t3 = 2 * temp[4] + temp[5];
int t4 = 2 * temp[6] + temp[7];
//在S盒中找到替换后的值
int num1 = s[t1][t2];
int num2 = s[t3][t4];
//分别进行四位四位的替换
for (int i = 0; i < 4; i++)
temp[i] = Replace[num1][i];
for (int i = 0; i < 4; i++)
temp[i + 4] = Replace[num2][i];
}
//g函数
int *g(int *temp, int *rcon)
{
//这个temp是密钥的右半部分,不能改动,要复制一个新的进行计算
int *t = new int[8];
for (int i = 0; i < 8; i++)
t[i] = temp[i];
//循环左移,即左右4位进行交换
for (int i = 0; i < 4; i++)
{
int tt = t[i + 4];
t[i + 4] = t[i];
t[i] = tt;
}
//移位后的右半部分进行字节替换
SubBytes(t);
//与轮常数异或
return OR_8(t, rcon);
}
//轮秘钥加
void AddRoundKey(int **mingwen, int **key)
{
for (int i = 0; i < 2; i++)
for (int j = 0; j < 8; j++)
mingwen[i][j] ^= key[i][j];
}
//行变换
void ShiftRows(int **temp)
{
//第一字节的右半部分和第二字节的右半部分进行替换
for(int i = 4;i < 8;i ++)
{
int t = temp[0][i];
temp[0][i] = temp[1][i];
temp[1][i] = t;
}
}
//4位的异或
int *OR_4(int *a, int *b)
{
int *t = new int[4];
for (int i = 0; i < 4; i++)
t[i] = a[i] ^ b[i];
return t;
}
//实现x*f(x)的函数
void x_fx(int last[4], int res[4])
{
//res是结果,last是上一步的结果
if (last[0] == 0)
{
//最高次为0
for (int i = 0; i < 3; i++)
//低三项分别升幂次
res[i] = last[i + 1];
}
else
{
//最高次为1
res[1] = last[2];
res[2] = last[3] == 1 ? 0 : 1;
res[3] = 1;
}
}
//乘法
int *multiply(int a[4], int b[4])
{
//储存结果的系数
int *result = new int[4];
for (int i = 0; i < 4; i++) result[i] = 0;
//记录下a*(x^n)
int x1fx[4] = {0};
x_fx(a, x1fx);//a*(x^1)=a*{0,0,1,0}=a*b3
int x2fx[4] = {0};
x_fx(x1fx, x2fx);//a*(x^2)=a*{0,1,0,0}=a*b2
int x3fx[4] = {0};
x_fx(x2fx, x3fx);//a*(x^3)=a*{1,0,0,0}=a*b1
//现在需要根据多项式a和b开始异或
if (b[0] == 1)//b1=={1,0,0,0}
for (int i = 0; i < 4; i++)
result[i] ^= x3fx[i];
if (b[1] == 1)//b2=={0,1,0,0}
for (int i = 0; i < 4; i++)
result[i] ^= x2fx[i];
if (b[2] == 1)//b3=={0,0,1,0}
for (int i = 0; i < 4; i++)
result[i] ^= x1fx[i];
if (b[3] == 1)//b4=={0,0,0,1}
for (int i = 0; i < 4; i++)
result[i] ^= a[i];
return result;
}
//列混淆
void MixColumns(int **mingwen)
{
int rule[4] = {0, 1, 0, 0};
int *m00 = new int[4]; // 第一行的前4个元素
int *m10 = new int[4]; // 第一行的后4个元素
int *m01 = new int[4]; // 第二行的前4个元素
int *m11 = new int[4]; // 第二行的后4个元素
for (int i = 0; i < 4; i++)
{
m00[i] = mingwen[0][i];
m10[i] = mingwen[0][i + 4];
m01[i] = mingwen[1][i];
m11[i] = mingwen[1][i + 4];
}
int *n00 = new int[4];
int *n10 = new int[4];
int *n01 = new int[4];
int *n11 = new int[4];
n00 = OR_4(m00, multiply(rule, m10));
n10 = OR_4(multiply(rule, m00), m10);
n01 = OR_4(m01, multiply(rule, m11));
n11 = OR_4(multiply(rule, m01), m11);
for (int i = 0; i < 4; i++)
{
mingwen[0][i] = n00[i];
mingwen[0][i + 4] = n10[i];
mingwen[1][i] = n01[i];
mingwen[1][i + 4] = n11[i];
}
}
int main()
{
//输入明文和密钥,存储在两个2x8的二维数组中,方便后续的密钥扩展(右半部分即key[1])
cout << "请输入明文(用空格分隔的16个数字):" << endl;
int **plaintext = new int *[2];
for (int i = 0; i < 2; i++)
{
plaintext[i] = new int[8];
for (int j = 0; j < 8; j++)
{
cin >> plaintext[i][j];
}
}
cout << "请输入密钥(用空格分隔的16个数字):" << endl;
int **key = new int *[2];
for (int i = 0; i < 2; i++)
{
key[i] = new int[8];
for (int j = 0; j < 8; j++)
{
cin >> key[i][j];
}
}
//密钥扩展算法,需要扩展出两个密钥key1和key2
int **key1 = new int *[2];
for (int i = 0; i < 2; i++)
key1[i] = new int[8];
int **key2 = new int *[2];
for (int i = 0; i < 2; i++)
key2[i] = new int[8];
//key1生成
key1[0] = OR_8(key[0], g(key[1], rcon1));
key1[1] = OR_8(key1[0], key[1]);
//key2生成
key2[0] = OR_8(key1[0], g(key1[1], rcon2));
key2[1] = OR_8(key2[0], key1[1]);
//第0轮的轮密钥加
AddRoundKey(plaintext, key);
// 第一轮
// 明文半字节代替
SubBytes(plaintext[0]);
SubBytes(plaintext[1]);
// 明文的行变换
ShiftRows(plaintext);
// 明文的列混淆
MixColumns(plaintext);
// 明文的轮密钥加
AddRoundKey(plaintext, key1);
// 第二轮
// 明文半字节代替
SubBytes(plaintext[0]);
SubBytes(plaintext[1]);
// 明文的行移位
ShiftRows(plaintext);
// 明文的轮密钥加
AddRoundKey(plaintext, key2);
cout << "最后的密文是:" << endl;
for (int i = 0; i < 2; i++)
for (int j = 0; j < 8; j++)
cout << plaintext[i][j] << ' ';
cout << endl;
return 0;
}
🐇python
# S盒
s = [[9, 4, 10, 11],
[13, 1, 8, 5],
[6, 2, 0, 3],
[12, 14, 15, 7]]
# 替换表
Replace = [[0, 0, 0, 0], [0, 0, 0, 1],
[0, 0, 1, 0], [0, 0, 1, 1],
[0, 1, 0, 0], [0, 1, 0, 1],
[0, 1, 1, 0], [0, 1, 1, 1],
[1, 0, 0, 0], [1, 0, 0, 1],
[1, 0, 1, 0], [1, 0, 1, 1],
[1, 1, 0, 0], [1, 1, 0, 1],
[1, 1, 1, 0], [1, 1, 1, 1]]
# 轮常数
rcon1 = [1, 0, 0, 0, 0, 0, 0, 0]
rcon2 = [0, 0, 1, 1, 0, 0, 0, 0]
def XR_8(a, b):
# a、b 分别是两个长度为 8 的数组,返回一个长度也为 8 的数组
t = [0] * 8 # 结果数组
for i in range(8):
t[i] = a[i] ^ b[i]
return t
# 字节替换
def SubBytes(temp):
# temp 是一个长度为8的数组,进行S盒替换
# 先计算出需要进行S盒替换的四位二进制数
t1 = 2 * temp[0] + temp[1]
t2 = 2 * temp[2] + temp[3]
t3 = 2 * temp[4] + temp[5]
t4 = 2 * temp[6] + temp[7]
# 进行 S 盒替换
num1 = s[t1][t2]
num2 = s[t3][t4]
# 将替换后的结果按四位四位赋值给temp
for i in range(4):
temp[i] = Replace[num1][i]
for i in range(4):
temp[i + 4] = Replace[num2][i]
# g函数
def g(temp, rcon):
# temp 是一个长度为8的数组,rcon是轮常数
t = temp.copy() # temp是密钥,不能改动,复制一个新的
# 进行循环左移
for i in range(4):
tt = t[i + 4]
t[i + 4] = t[i]
t[i] = tt
# 进行 S 盒替换
SubBytes(t)
# 进行轮常数异或
return XR_8(t, rcon)
# 轮密钥加
def AddRoundKey(mingwen, key):
for i in range(2):
for j in range(8):
mingwen[i][j] ^= key[i][j]
# 行变换
def ShiftRows(temp):
# 第一字节的右半部分和第二字节的右半部分进行替换
for i in range(4, 8):
t = temp[0][i]
temp[0][i] = temp[1][i]
temp[1][i] = t
# 4位的异或
def OR_4(a, b):
# a、b 分别是两个长度为 4 的数组,返回一个长度也为 4 的数组
t = [0] * 4 # 结果数组
for i in range(4):
t[i] = a[i] ^ b[i]
return t
def x_fx(f, a):
# 进行有限域上的多项式除法运算,用于求解一个元素的逆元
if a[0] == 0:
for i in range(3): # 定义一个长度为4的数组f表示一个3次多项式
f[i] = a[i + 1]
else:
f[1] = a[2]
f[2] = 0 if a[3] == 1 else 1
f[3] = 1
def multiply(a, b):
# 在有限域 GF(2^4) 上的多项式乘法运算
# 记录下f^n
f = [0] * 4
x_fx(f, a)
f2 = [0] * 4
x_fx(f2, f)
f3 = [0] * 4
x_fx(f3, f2)
# 现在需要根据多项式a和b开始异或
result = [0] * 4 # 储存结果的系数
if b[0] == 1:
for i in range(4):
result[i] ^= f3[i]
if b[1] == 1:
for i in range(4):
result[i] ^= f2[i]
if b[2] == 1:
for i in range(4):
result[i] ^= f[i]
if b[3] == 1:
for i in range(4):
result[i] ^= a[i]
return result
# 列混淆
def MixColumns(mingwen):
rule = [0, 1, 0, 0]
m00 = mingwen[0][:4]
m10 = mingwen[0][4:]
m01 = mingwen[1][:4]
m11 = mingwen[1][4:]
n00 = OR_4(m00, multiply(rule, m10)) # 乘法结果是1011
n10 = OR_4(multiply(rule, m00), m10) # 0101
n01 = OR_4(m01, multiply(rule, m11)) # 0100
n11 = OR_4(multiply(rule, m01), m11) # 0010
mingwen[0][:4] = n00
mingwen[0][4:] = n10
mingwen[1][:4] = n01
mingwen[1][4:] = n11
if __name__ == "__main__":
mingwen_str = "0110111101101011"
key_str = "1010011100111011"
mingwen = [[int(mingwen_str[i * 8 + j]) for j in range(8)] for i in range(2)]
key = [[int(key_str[i * 8 + j]) for j in range(8)] for i in range(2)]
# 密钥扩展算法,由于只有三轮加密,第一轮只使用了原始key
key1 = [[0] * 8 for _ in range(2)]
key2 = [[0] * 8 for _ in range(2)]
key1[0] = XR_8(key[0], g(key[1], rcon1))
key1[1] = XR_8(key1[0], key[1])
key2[0] = XR_8(key1[0], g(key1[1], rcon2))
key2[1] = XR_8(key2[0], key1[1])
# 第零轮
# 轮密钥加
AddRoundKey(mingwen, key)
# 第一轮
# 明文半字节代替
SubBytes(mingwen[0])
SubBytes(mingwen[1])
# 明文的行移位
ShiftRows(mingwen)
# 明文的列混淆
MixColumns(mingwen)
# 明文的轮密钥加
AddRoundKey(mingwen, key1)
# 第二轮
# 明文半字节代替
SubBytes(mingwen[0])
SubBytes(mingwen[1])
# 明文的行移位
ShiftRows(mingwen)
# 明文的轮密钥加
AddRoundKey(mingwen, key2)
# 输出结果
print("密文为:")
for i in range(2):
for j in range(8):
print(mingwen[i][j], end=' ')

- 以上若有理解错的地方欢迎指正!
更多推荐
 已为社区贡献21条内容
已为社区贡献21条内容







所有评论(0)