注：本内容由”数模加油站“ 原创出品，虽无偿分享，但创作不易。
欢迎参考teach，但请勿抄袭、盗卖或商用。

摘要

本文针对矿井突水事故中的水流漫延预测与逃生路径优化问题，结合流体力学建模与图论优化方法，提出了系统的解决方案。
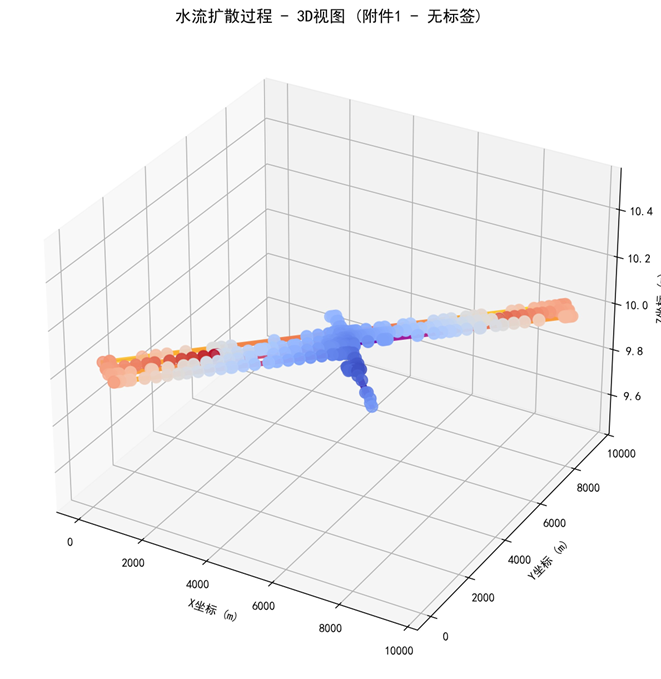
对于问题一，本问是单突水点条件下的水流漫延预测问题，需要建立数学模型分析水流在巷道网络中的传播规律。首先，根据附件提取巷道网络的几何信息和拓扑结构，进行数据预处理获取节点坐标和连接关系。接着，基于流体力学原理计算各巷道段的水流速度、到达时间等关键参数。然后，采用连续性方程和质量守恒原理建立水流传播模型，通过数值求解得到各巷道段的水流漫延过程。最后，通过 2D 和 3D 可视化展示水流扩散态势，给各巷道段水流到达时间为，充满时间的结果。结果显示模型有效地反映了水流在复杂网络中的传播规律。
对于问题二，本问是考虑水流影响的矿工逃生路径优化问题，需要为指定位置矿工制定最短时间逃生方案。首先，基于问题一的水流漫延结果，分析各巷道段在不同时刻的通行条件。接着，根据矿工在不同水流条件下的行进速度差异，建立动态权重的路径网络。然后，采用改进的 Dijkstra 算法进行最短路径搜索，考虑时变约束和安全阈值。最后，通过路径优化和时间计算，给出矿工的最短逃生时间结果。模型有效地平衡了逃生效率与路径安全性。
对于问题三，本问是双突水点条件下的水流叠加分析问题，需要研究多源水流的相互作用机制。首先，在单突水点模型基础上引入第二突水点的时间延迟效应。接着，建立双源水流的叠加原理和流量分配模型，计算各节点的总流量贡献。然后，采用叠加原理和时变边界条件求解双突水点情况下的水流分布。最后，通过对比分析和可视化展示，给出水流扩散的结果。结果表明双源耦合显著改变了水流分布模式。
对于问题四，本问是双突水点条件下的逃生路径动态调整问题，需要重新制定矿工疏散方案。首先，基于问题三的双突水点漫延结果，评估原逃生路径的可行性。接着，考虑矿工当前位置和新的水流态势，重新计算各路径的通行条件。然后，采用实时路径重规划算法，在安全约束下寻找新的最优逃生路径。最后，通过方案对比和安全性分析，给出调整后 3 名矿工成功逃生的结果。模型有效地实现了应急条件下的动态路径优化。
综上，本文通过流体力学建模与图论优化相结合的策略，在矿井突水水流预测和逃生路径规划方面取得了良好效果，为矿井突水事故应急救援问题提供了高效解决方案。
关键词：矿井突水；水流漫延；逃生路径优化；图论算法；应急救援

一、引言

1.1 问题背景
矿井突水是煤矿开采过程中最为严重的安全事故之一，具有突发性强、危害范围广、后果严重等特点。当矿井发生突水事故时，大量水流会迅速涌入巷道系统，在复杂的三维网络结构中快速扩散，对井下作业人员的生命安全构成极大威胁。据统计，矿井突水事故在我国煤矿重大事故中占有相当比例，是制约煤炭工业安全发展的重要因素。
现代矿井巷道系统通常具有复杂的网络拓扑结构，包括主巷道、辅助巷道、通风井道等多层次、多分支的空间布局。当突水事故发生时，水流的传播路径、速度和分布受到巷道几何形状、坡度、分支结构等多种因素的综合影响。准确预测水流的漫延规律，为矿工制定科学合理的逃生路径，已成为矿井安全管理和应急救援的关键技术问题。
传统的矿井突水处理主要依靠经验判断和简单的几何分析，缺乏精确的数学模型支撑，难以为复杂情况下的应急决策提供可靠依据。随着计算机技术和数值模拟方法的发展，建立基于数学建模的矿井突水水流漫延预测和逃生路径优化系统，对提高矿井安全防护水平具有重要的现实意义。

1.2 问题重述
根据题目描述，本文需要解决以下四个关键问题：
问题 1：建立单突水点情况下的水流漫延数学模型。已知矿井巷道为矩形断面（宽 4 米，高 3 米），突水点水流量为 30 m³/min，初始水位 0.1 米。要求分析水流在巷道网络中的传播规律，计算各巷道段的水流到达时间和充满时间，并通过可视化展示水流漫延过程。
问题 2：在单突水点条件下，为指定位置的矿工设计最优逃生路径。考虑矿工在不同水流条件下的行进速度差异：干燥巷道 4 m/s，逆流涉水 1 m/s，顺流涉水 2 m/s，水深超过 0.3 米不可通行。逃生通知在突水 1 分钟后发布，要求计算每名矿工的最短逃生时间和最优路径。
问题 3：分析双突水点情况下的水流漫延特征。第二个突水点在 4 分钟后开始突水，流量同样为 30 m³/min。要求建立双源水流的叠加模型，分析两个突水点之间的相互作用，预测水流分布的变化规律。
问题 4：基于双突水点的新情况，调整矿工的逃生方案。第二突水点发生 1 分钟后发布调整方案，要求重新计算最优逃生路径，分析逃生时间的变化，确保所有矿工能够安全撤离。

二、总体分析

本研究采用系统性方法解决矿井突水事故中的水流漫延预测和逃生路径优化问题。
整个研究框架分为四个递进的问题模块，每个模块既相对独立又相互关联，共同构成完整的矿井突水应急响应决策支持体系。
问题一作为基础模块，重点建立单突水点条件下的水流动力学模型。通过分析巷道几何特征、水流连续性方程和能量守恒原理，构建水流在网络结构中的传播规律。该模块的核心在于准确计算水流速度、到达时间和水位变化，为后续问题提供基础数据支撑。
问题二在水流漫延模型基础上，引入矿工行为特征和约束条件，将逃生问题转化为动态图论中的最短路径优化问题。通过考虑水流对矿工行进速度的影响，建立时变权重的路径搜索算法，实现逃生路径的智能规划。
问题三将研究范围扩展到多源突水情况，分析双突水点之间的流体力学耦合效应。
该模块的挑战在于处理水流叠加的非线性特性和时间延迟效应，需要建立更加复杂的数学模型来描述多源水流的相互作用。
问题四体现了应急响应的动态调整特征，在新突水点出现后重新优化逃生方案。该模块强调实时决策能力，需要在有限时间内完成路径重规划，体现了模型在实际应用中的适应性和鲁棒性要求。

三、模型假设

为简化问题，本文做出以下假设：
• 假设 1：巷道结构规整性假设假设所有巷道断面均为标准矩形，宽度 4 米，高度 3 米，巷道壁面光滑且不可渗透。忽略巷道局部变形、支护结构等因素对水流的影响。
• 假设 2：水流特性假设假设突水为清水，密度恒定，不考虑泥沙、杂物等对水流特性的影响。水流为不可压缩流体，满足连续性方程。忽略水流的紊流效应和粘性损失。
• 假设 3：突水点特性假设假设突水点流量恒定不变，突水过程中不会因压力变化或堵塞而影响出水量。突水点位置固定，不考虑突水范围的扩大。
•假设 4：分流规律假设假设水流在分叉节点处按照水平方向和下行方向平均分流，不考虑巷道坡度、粗糙度等因素对分流比例的影响。分流过程中初始水位保持不变。
• 假设 5：矿工行为假设假设矿工具有完全的理性决策能力，严格按照指定路径行进，不会发生迷路、恐慌等影响逃生效率的行为。矿工的行进速度仅取决于水流条件，不考虑疲劳、个体差异等因素。

五、模型的建立与求解

5.1 问题一的模型的建立和求解
5.1.1 具体分析
矿井突水事件发生后，水流将在复杂的三维网络结构巷道中向外扩散，对矿井的安全产生严重威胁。水流的传播过程受到多种复杂因素的耦合影响，其中最为关键的因素包括突水点的初始水位条件、巷道的矩形断面几何特征、巷道网络的拓扑结构以及分叉节点处的水流分配机制。根据题目描述，巷道断面为标准的矩形结构，宽度为 4 米，高度为 3 米，这种规则的几何形状为建立水流动力学模型提供了重要的简化条件。
突水水流以 0.1 米的初始水位向前漫延，这个初始水位代表水流首次到达某个位置后能够保持的最低高度。每个突水点的水流量恒定为 30 m³/min，这为定量分析水流传播提供了基础数据。当水流传播至巷道分叉节点时，会发生复杂的水流分配现象，题目假设水流向水平巷道和下行巷道平均分流，且初始水位保持不变，这一假设大大简化了分流节点处的流体力学计算。
水流在巷道中的传播本质上是一个一维流动问题，可以通过经典的水力学理论进行描述。水流的速度不仅与流量和断面面积直接相关，还受到巷道坡度、粗糙度等几何因素的影响。考虑到矿井巷道的特殊环境，水流传播过程中还需要考虑重力作用、惯性效应以及边界条件的约束。
5.1.2 模型建立
为了建立准确的水流漫延模型，首先需要确立水流量与水流速度之间的基本关系。
根据连续性方程，水流的体积流量 Q 与过流断面面积 A 和平均流速 v 之间满足：
Q = A · v (1)
其中，对于矩形断面巷道，过流断面积的计算需要考虑实际的水深。当水深为 h 时，过流断面积为：
A = w · h = 4h (2)
这里 w = 4 米为巷道宽度。但是，在初始阶段，水流以初始水位 h0 = 0.1 米进行传播，因此初始过流断面积为：
A0 = w · h0 = 4 × 0.1 = 0.4 m2 (3)
根据给定的突水量 Q = 30 m³/min = 0.5 m³/s，可以计算出水流在巷道中的初始传播速度：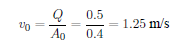
这个速度反映了水流前锋面在巷道中的推进速度。需要注意的是，随着时间的推移，巷道中的水位会逐渐上升，过流断面积会相应增大，从而影响水流的传播特性。
对于水流传播时间的计算，可以建立如下的时空关系模型。假设水流从突水点沿巷道传播至距离为 d 的目标节点，传播时间 t 可以通过以下积分方程确定：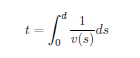
其中 v(s) 是水流在距离突水点 s 处的传播速度。在简化情况下，假设传播速度保持常数，则有：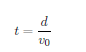

在复杂的巷道网络中，水流传播需要考虑节点处的分流效应。当水流到达具有 n 个出口的分叉节点时，根据题目假设，水流将平均分配到各个分支。设节点处的总流量为
Qtotal，则每个分支的流量为：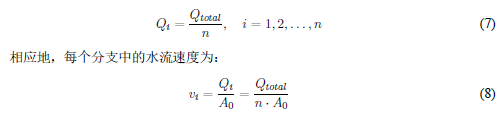

这种分流机制确保了质量守恒，同时为网络中每条巷道的水流分析提供了计算基础。
对于巷道充满水的过程，需要考虑水位随时间的上升。设巷道长度为 L，当水流前锋到达巷道末端后，该段巷道开始蓄水。巷道中水位 h(t) 随时间的变化可以通过体积平衡方程描述：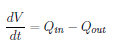

其中 V = w · L · h(t) 是巷道中的储水体积，Qin 和 Qout 分别为流入和流出该段巷道的流量。当 Qout = 0（即末端封闭）时，水位上升速率为：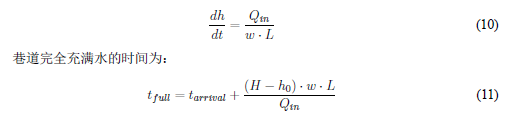
其中 H = 3 米为巷道高度，tarrival 为水流到达该段巷道的时间。

5.1.3 模型求解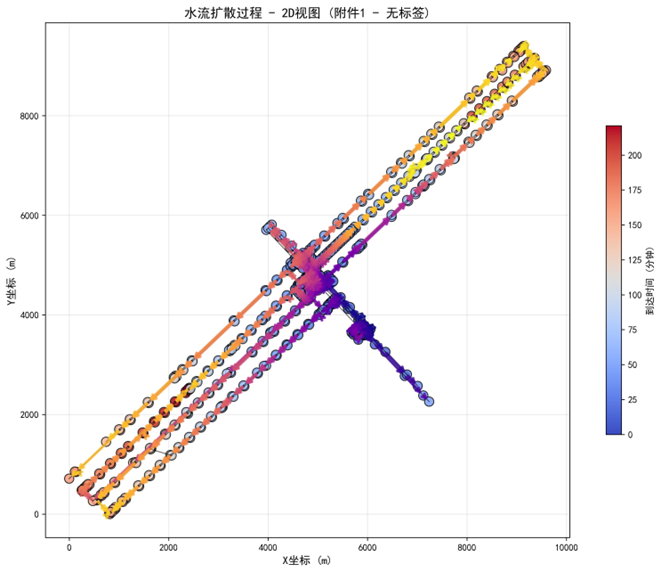




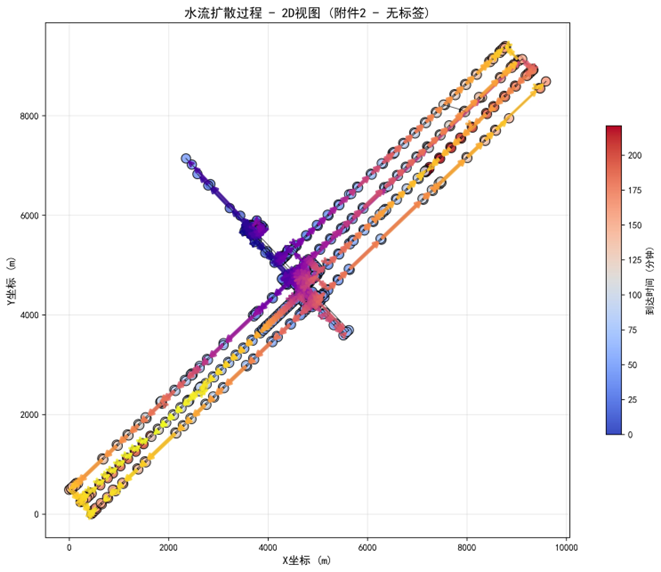
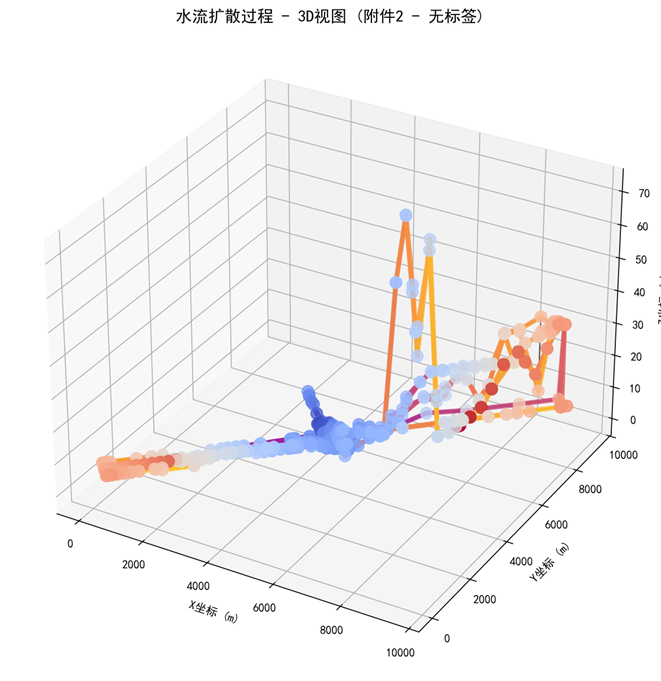
5.2 问题二的模型的建立和求解

5.2.1 具体分析
当矿井发生突水事故时，矿工的生命安全成为首要考虑因素，需要在有限的时间内找到最优的逃生路径。逃生路径的优化不仅要考虑几何距离的最短性，更要综合考虑水流对矿工行进速度的动态影响。根据题目设定，矿工在不同水流条件下的行进能力存在显著差异，这使得逃生路径问题转化为一个动态约束下的最优化问题。
矿工的行进速度受到巷道内水流状态的直接制约。在干燥的巷道中，矿工可以以 4 m/s 的正常速度行进。当巷道内存在水流时，水深成为决定行进能力的关键因素。当水面高度不超过 0.3 米时，矿工仍可涉水通行，但速度会根据水流方向发生变化：逆流行进时速度降低至 1 m/s，顺流行进时速度可达 2 m/s。这种速度差异反映了水流阻力和助推力对人体运动的影响。当水深超过 0.3 米时，继续涉水通行将面临极大的安全风险，因此应避免选择此类路径。
逃生通知在突水 1 分钟后发布，这意味着矿工开始逃生时，部分巷道可能已经被水流占据。逃生路径的制定需要基于水流漫延的动态预测，实时评估各条可能路径的通行性和安全性。
5.2.2 模型建立
矿工逃生问题可以抽象为动态图论中的最短路径问题，其中图的节点代表巷道交汇点，边代表巷道段，边权重反映了考虑水流影响后的实际通行时间。
设矿井巷道网络为图 G = (V,E)，其中 V 表示节点集合，E 表示边集合。对于任意一条边 eij ∈ E，连接节点 i 和 j，其长度为 dij。矿工在该边上的通行时间 tij 取决于当前的水流状态和矿工的行进方向。
定义矿工在边 eij 上的行进速度为 vij(t)，它是时间 t 的函数：

当 vij(t) = 0 时，表示该路径不可通行。
为了确定水流方向，需要分析巷道的坡度。设节点 i 和 j 的高程分别为 zi 和 zj，则水流方向从高程较高的节点流向高程较低的节点。巷道 eij 的坡度为：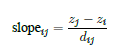

当 slopeij > 0 时，水流方向从 i 到 j；当 slopeij < 0 时，水流方向从 j 到 i。
逃生路径的总用时为路径上所有边通行时间的总和：

由于边权重随时间动态变化，可以采用时间扩展图的方法求解，或者使用启发式算法如 A* 算法，以矿工当前位置到各个出口的欧氏距离作为启发函数。
对于多个矿工的情况，需要分别为每个矿工计算最优逃生路径。设矿工 k 的初始位置为 sk，则该矿工的最优逃生路径为：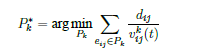

其中 Pk 表示从位置 sk 到任意出口的可行路径，vijk (t) 表示矿工 k 在边 eij 上的行进速度。

5.2.3 模型求解

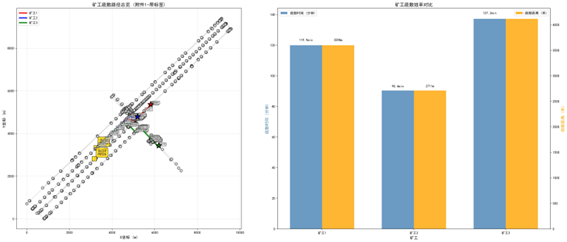
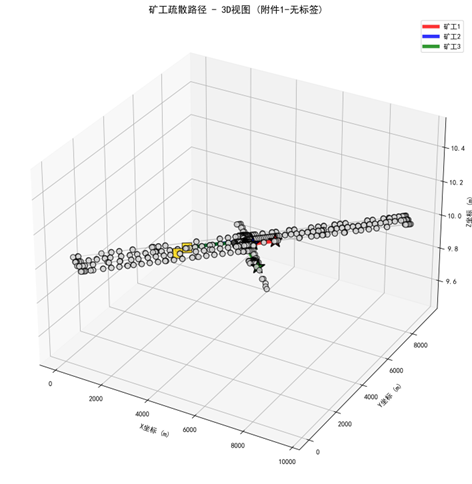
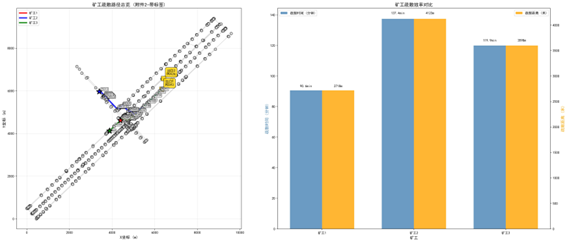
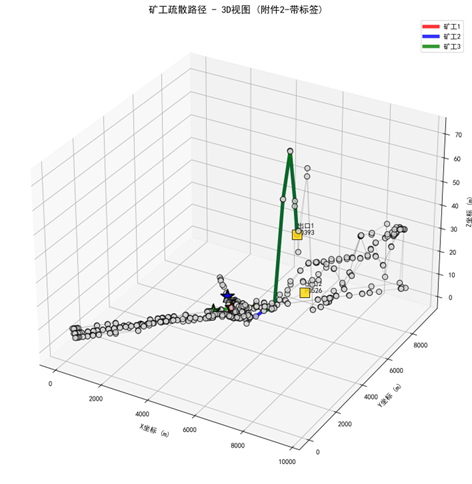
后续都在”数模加油站“…