“降维就像给机器装上眼睛——它最终看到的是森林，而不仅仅是树木。”

为什么降维很重要

想象一下，试图通过微型望远镜探索星系——这就是机器学习模型处理原始高维数据时的感受。降维将复杂的高维数据集转换为更简单的形式，帮助人类和机器发现隐藏的模式。

但是有这么多可用的技术，您应该使用哪一种呢？

在此博客中，我们将从以下方面比较 PCA、t-SNE 和 UMAP ：

• 直觉
• 工作原理
• 真实用例
• 视觉示例
• Python 实现
• 优点、缺点和最佳方案

💡 是的，我们将用一份备忘单、比较视觉效果和精心挑选的资源来加深您的理解。

1.主成分分析（PCA）

直觉

PCA将数据投影到一个新的坐标系中，其中的轴（主成分）使方差最大化。这就像旋转数据集，使其与能够捕捉最大扩散的方向对齐。

当您需要速度、可解释性以及与 ML 模型的兼容性时，请使用 PCA 。

PCA 的工作原理

1. 标准化数据
2. 计算协方差矩阵
3. 查找特征向量和特征值
4. 将数据投影到 top-k 个组件上

真实用例

• 金融：风险建模、信用评分
• 基因组学：减少基因表达特征
• 预处理：聚类或建模之前

Python代码

from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
import seaborn as sns
import matplotlib.pyplot as plt

iris = load_iris()
X = StandardScaler().fit_transform(iris.data)
y = iris.target

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], hue=iris.target_names[y])
plt.title("PCA on Iris Dataset")
plt.show()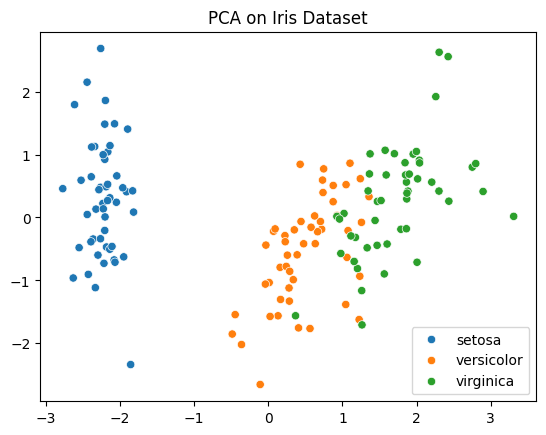

优点

• 非常快
• 保留全局结构
• 机器学习友好型

缺点

• 仅线性
• 没有聚类洞察

2. t-SNE（t分布随机邻域嵌入）

直觉

t-SNE 将高维数据映射到二维或三维空间，保留局部邻域- 这意味着相似的点保持接近。

使用 t-SNE 进行聚类可视化和探索性分析。

t-SNE 的工作原理

1. 计算高维空间中的相似性
2. 使用 Student-t 分布对低维相似性进行建模
3. 尽量减少两者之间的分歧

真实用例

• 计算机视觉：可视化 CNN 嵌入
• 生物信息学：细胞类型聚类
• 分析：应用行为细分

Python代码

from sklearn.manifold import TSNE

tsne = TSNE(n_components=2, random_state=42, perplexity=30, n_iter=300)
X_tsne = tsne.fit_transform(X)

sns.scatterplot(x=X_tsne[:, 0], y=X_tsne[:, 1], hue=iris.target_names[y])
plt.title("t-SNE on Iris Dataset")
plt.show()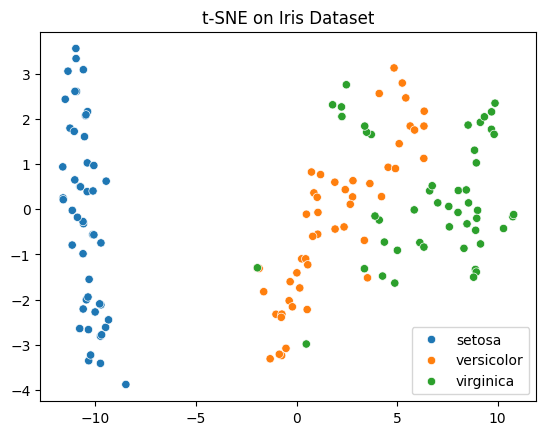

优点

• 非常适合可视化集群
• 很好地捕捉局部结构

缺点

• 计算成本高昂
• 无逆变换或机器学习兼容性
• 对超参数敏感

3. UMAP（均匀流形近似和投影）

直觉

UMAP 利用图论和流形学习，保留局部和部分全局结构。它就像 t-SNE 的更智能、更快速的“表亲”。

当您需要速度 + 集群可视化 + 可扩展性时，请使用 UMAP 。

UMAP 的工作原理

1. 在高维空间中构建模糊图
2. 优化低暗空间的布局
3. 以最小的扭曲保留关系

真实用例

• NLP：词嵌入可视化
• 医学成像：特征提取
• 营销：客户细分