目录

一、前言

1.Transformer并非完美

二、Mamba的原理

1.状态空间模型（State Space Model，SSM）的基本原理

2.利用Zero-order hold对SSM进行离散化处理

（1）Zero-order hold(零阶状态保持)

（2）如何对SSM进行离散化呢？

3.直接使用SSM做语言序列预测的弊端

4.Mamba如何实现呢？

三、Mamba原理代码及其可视化实现

四、致谢

---

一、前言

1.Transformer并非完美

Transformer的输入窗口长度有限，且模型规模随输入序列长度平方次增长 。在处理长序列时，计算成本高。

Transformer VS. RNN

模型	Transformer	RNN
优点	构建灵活，易并行、易拓展	串行输入，理论上可以处理无限长序列
局限	并行输入，输入长度有限，模型规模随输入序列长度平方增长	训练长序时容易出现梯度消失或爆炸问题，且输入被过度压缩，模型能力受限

为了避免模型规模随序列长度二次增长，同时克服RNN的局限性，近年来研究者提出了多种RNN变体。其中基于选择状态空间模型(Selective State Space Model,SSSM)的Mamba模型（《Mamba: Linear-Time Sequence Modeling with Selective State Spaces》，原文：https://arxiv.org/pdf/2312.00752）引发了广泛关注。

二、Mamba的原理

Mamba在状态空间模型（State Space Model,SSM）的基础上加入选择机制，确保其可以高效处理长序列，并且还可以达到与Transformer匹敌的模型能力。

Mamba的底层是Selective State Space Model,而状态空间模型（State Space Model）又是什么？State Space Model是控制里的知识，而这可能就是让很多人读Mamba论文时云里雾里的主要原因了吧。下面我们先来讲解State Space Model!

1.状态空间模型（State Space Model，SSM）的基本原理

SSM，是将一个n阶系统，用n个一阶等式进行矩阵表达，它实际上是一种空间转换的形态。

举个例子，在如图所示的弹簧振子系统中

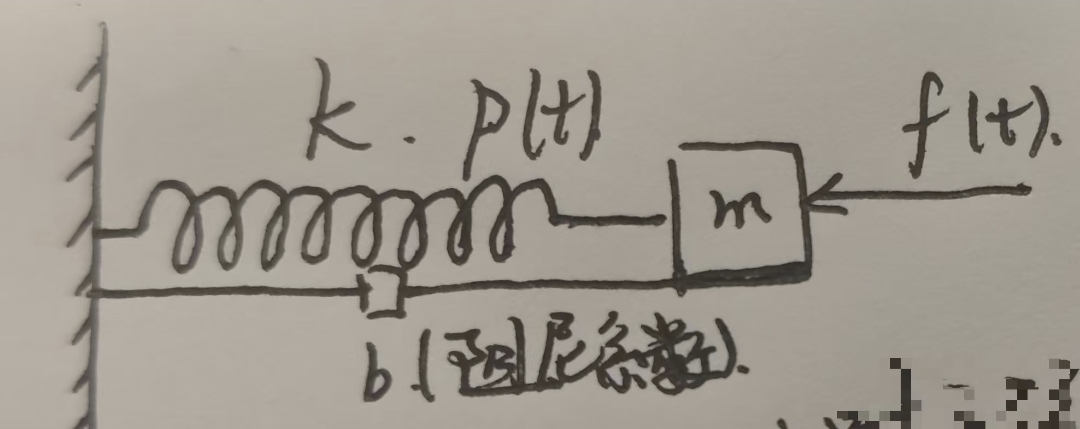
用表示对弹簧施加的外力，用表示物块m产生的位移

那么，对于该弹簧振子系统，我们有

那也就是说，我们对这个弹簧振子系统施加了多少力，我们就能计算出物块的位置，而位置序列与NLP中的语言序列都是序列，我们是否也可以用这种办法来预测（表达、计算）呢？

好像从这个二阶ode来看，位置序列和token序列并没有多大联系，应该是不能的。那么，我们继续做变换

对于二阶方程，我们称其为二阶系统

令，，那么很自然地有，从而有

而这个方程中的矩阵，每一行都是一阶量

SSM实际上是描述系统的另一种形式，称，为系统的状态

同理，输出，而在大模型领域，我们一般定义输出为，输入为

令   ，       ，   

 ， 

而这就是在Mamba论文中出现的第一个公式，State Space Model(SSM)

而SSM与语言序列最大的gap在于，语言序列是离散的，h(t)是连续变量，这并不能用于NLP，那么我们将上面的h(t)进行离散化处理。

2.利用Zero-order hold对SSM进行离散化处理

（1）Zero-order hold(零阶状态保持)

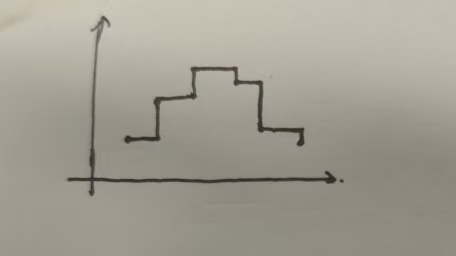
对于离散的点，如图所示

我们想要让他们连起来，采用Zero-order hold的效果是这样的：

（2）如何对SSM进行离散化呢？

由此，我们得到了Mamba论文中的第二个公式，离散化处理。

对于之前的SSM是连续的，没有办法做NLP中的语言序列，那么我们离散化后的我们就可以当作是下一个token,即，。

3.直接使用SSM做语言序列预测的弊端

我们有推导过程可知，A和B都是固定的，及根据时间是不变的（线性时不变），那么这样就会导致模型的参数一直保持不变，就类似与之前的RNN，那么Mamba对此做出了改进。

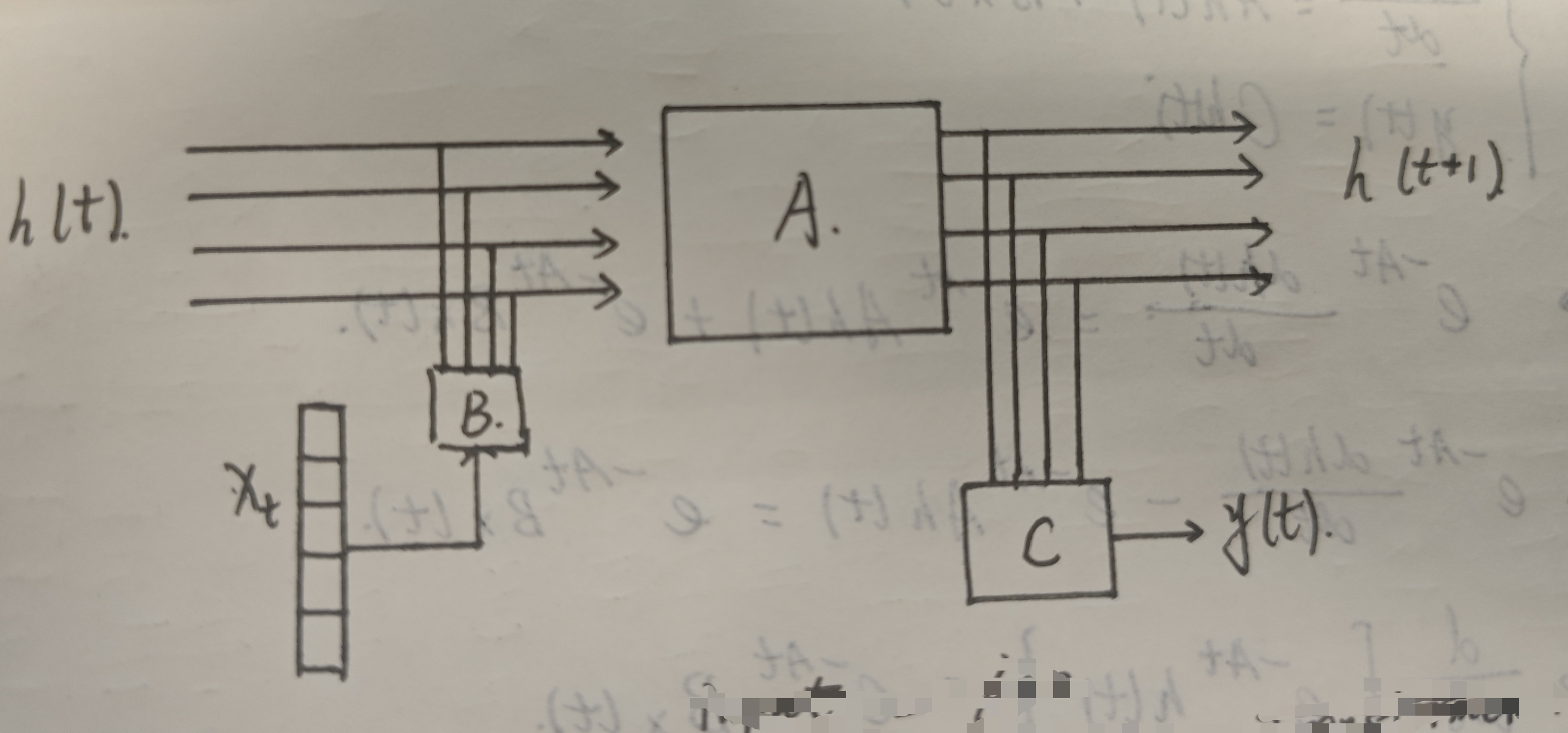
这就是之前使用SSM或者是RNN做语言序列处理时的模型结构图，我们假设input = 100，将SSM/RNN与Transformer两者进行对比

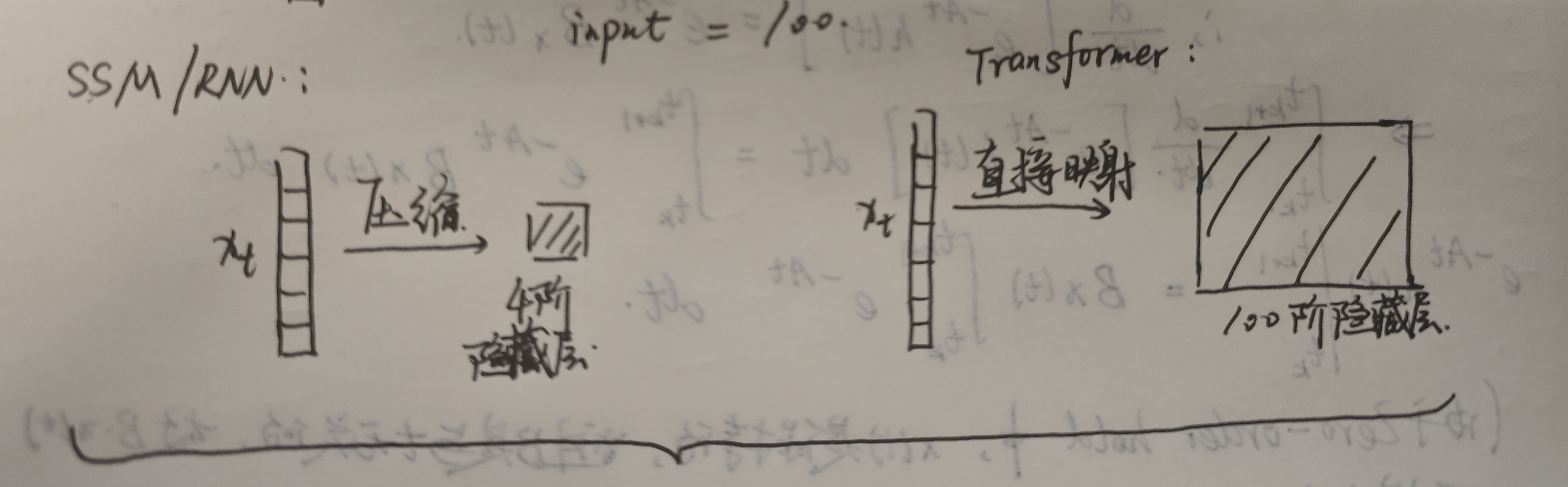
不难发现，SSM/RNN是直接将长序列压缩了，而这很可能会损失很多有价值的语义信息；而Transformer是不论输入维度有多大，直接进行映射，该例子中直接映射到100阶的隐藏层上，而SSM/RNN压缩到4阶隐藏层上，显然，就语义信息的完整度上，Transformer是完胜的，但是这也就造成了Transformer计算复杂度随序列长度呈现平方增长。

那么，我们能不能将两者折中呢？

训练出另一个模型，比SSM/RNN选择更多一些，也不是像Transformer那样，什么都要。而这个模型就是Mamba!

4.Mamba如何实现呢？

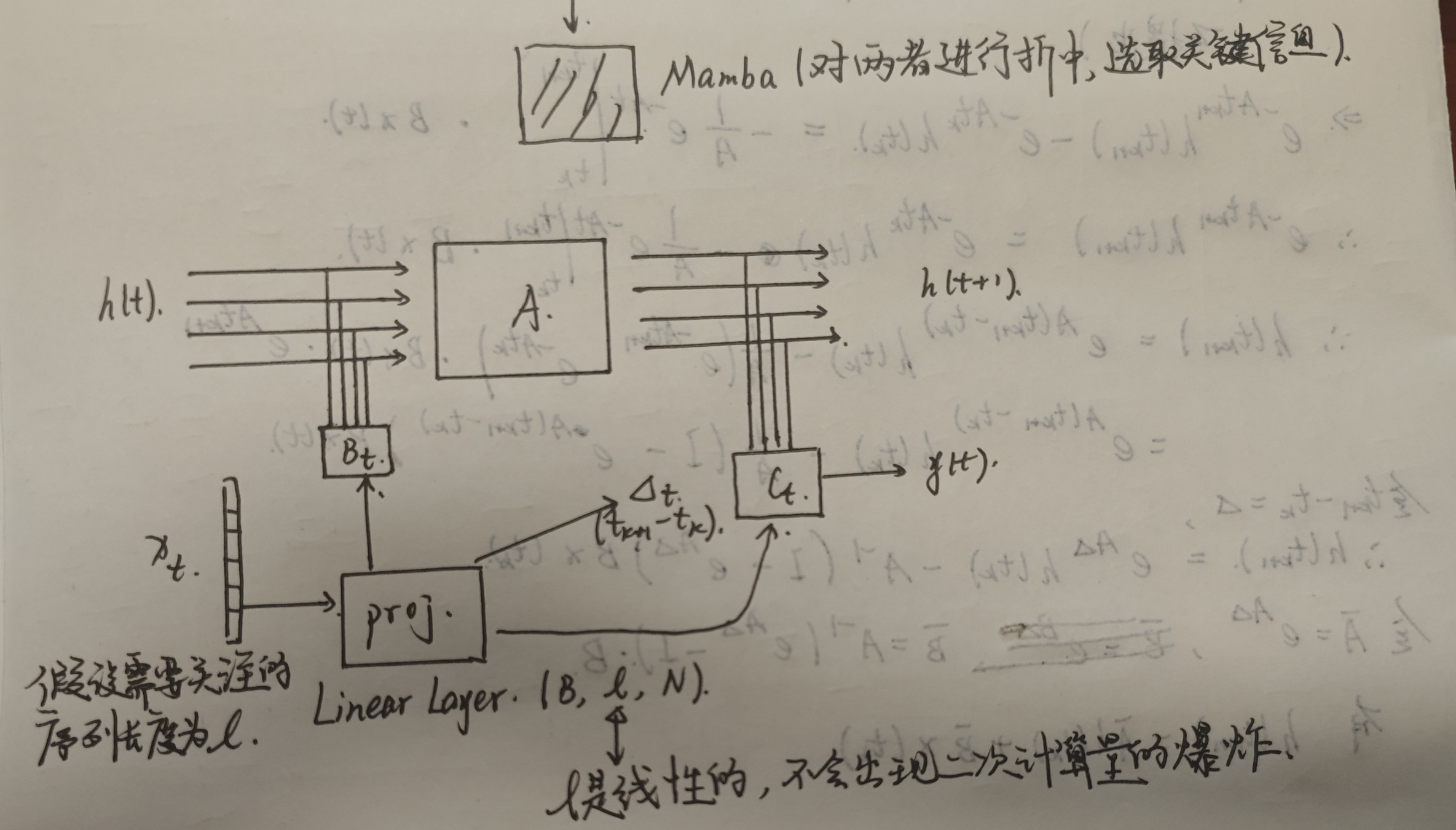
Mamba的做法如上图所示，而这种做法又与LSTM似曾相识

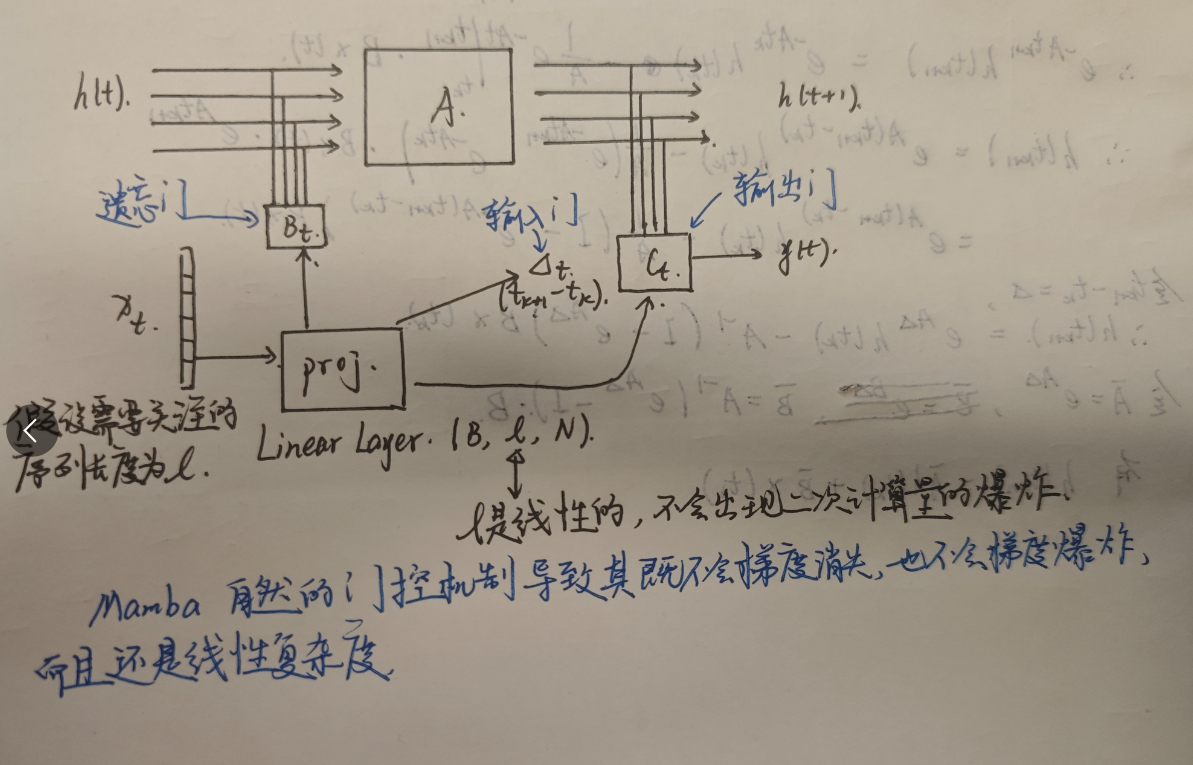
我们知道Mamba是从连续信号推导得来的，那么Mamba适合做前后有一定联系的预测，但对于前后联系不紧密或者根本没有联系的呢？

比如说在论文中是用基因做的实验，但是基因前后并没有什么关联，那么我们是否能将Mamba进行改进，创造出新的“Mamba”以适应前后并无联系呢？

三、Mamba原理代码及其可视化实现

"""
Mamba状态空间模型(SSM)实现
本代码实现了一个基于JAX的状态空间模型，用于模拟弹簧-质量-阻尼器系统
并生成动态可视化动画
"""

from functools import partial
import jax
import jax.numpy as np
from jax.numpy.linalg import inv

def example_mass(k, b, m):
    """
    生成弹簧-质量-阻尼器系统的状态空间模型矩阵
    
    参数:
        k: 弹簧常数 (N/m)
        b: 阻尼系数 (N·s/m) 
        m: 质量 (kg)
    
    返回:
        A: 状态转移矩阵 (2x2)
        B: 输入矩阵 (2x1)
        C: 输出矩阵 (1x2)
    
    系统方程:
        ẋ₁ = x₂                    # 位置对时间的导数 = 速度
        ẋ₂ = -(k/m)x₁ - (b/m)x₂ + u/m  # 加速度方程 (牛顿第二定律)
    """
    # 状态转移矩阵A: 描述系统内部动态
    A = np.array([[0, 1], [-k/m, -b/m]])
    
    # 输入矩阵B: 描述外部输入对状态的影响
    B = np.array([[0], [1.0/m]])
    
    # 输出矩阵C: 描述从状态到输出的映射
    C = np.array([[1.0, 0]])  # 只观测位置x₁
    
    return A, B, C

@jax.vmap
def example_force(t):
    """
    生成示例输入力函数u(t)
    使用JAX的vmap装饰器实现向量化计算
    
    参数:
        t: 时间点
        
    返回:
        力的大小，为正弦波与阶跃函数的乘积
    """
    x = np.sin(10 * t)  # 10Hz正弦波
    return x * (x > 0.5)  # 只保留大于0.5的部分

def discretize(A, B, C, step):
    """
    将连续时间状态空间模型离散化
    使用双线性变换(Bilinear Transform)方法
    
    参数:
        A, B, C: 连续时间系统矩阵
        step: 离散化步长
        
    返回:
        Ab, Bb, Cb: 离散化后的系统矩阵
        
    双线性变换公式:
        s → (2/T) * (z-1)/(z+1)
        其中T是采样时间
    """
    # 单位矩阵
    I = np.eye(A.shape[0])
    
    # 计算双线性变换的中间矩阵
    BL = inv(I - (step / 2.0) * A)
    
    # 离散化状态转移矩阵
    Ab = BL @ (I + (step / 2.0) * A)
    
    # 离散化输入矩阵
    Bb = (BL * step) @ B
    
    # 输出矩阵保持不变
    return Ab, Bb, C

def scan_SSM(Ab, Bb, Cb, u, x0):
    """
    使用JAX的scan函数实现离散状态空间模型的递归计算
    scan函数提供高效的前向传播，适合序列处理
    
    参数:
        Ab, Bb, Cb: 离散化系统矩阵
        u: 输入序列 [L, 1]
        x0: 初始状态
        
    返回:
        (final_state, outputs): 最终状态和输出序列
    """
    def step(x_k_l, u_k):
        """
        单步状态更新函数
        
        参数:
            x_k_l: 当前状态 x[k-1]
            u_k: 当前输入 u[k]
            
        返回:
            x_k: 下一状态 x[k]
            y_k: 当前输出 y[k]
        """
        # 状态更新: x[k] = Ab * x[k-1] + Bb * u[k]
        x_k = Ab @ x_k_l + Bb @ u_k
        
        # 输出计算: y[k] = Cb * x[k]
        y_k = Cb @ x_k
        
        return x_k, y_k
    
    # 使用JAX的scan函数进行高效的序列计算
    return jax.lax.scan(step, x0, u)

def run_SSM(A, B, C, u):
    """
    运行完整的状态空间模型仿真
    
    参数:
        A, B, C: 连续时间系统矩阵
        u: 输入序列 [L]
        
    返回:
        y: 输出序列 [L] - 系统的位置响应
    """
    L = u.shape[0]  # 序列长度
    N = A.shape[0]  # 状态维度
    
    # 根据序列长度确定离散化步长
    # 假设总仿真时间为1秒，步长为1/L
    Ab, Bb, Cb = discretize(A, B, C, step=1.0 / L)

    # 运行递归计算
    # 将输入重塑为列向量 [L, 1]，初始状态为零向量
    _, outputs = scan_SSM(Ab, Bb, Cb, u[:, np.newaxis], np.zeros((N,)))
    
    # 返回输出序列
    return outputs

def example_ssm():
    """
    状态空间模型示例和动画演示
    演示弹簧-质量-阻尼器系统对周期性力的响应
    """
    # 创建状态空间模型
    # k=40: 弹簧常数 (N/m), b=5: 阻尼系数 (N·s/m), m=1: 质量 (kg)
    ssm = example_mass(k=40, b=5, m=1)

    # 生成时间序列
    L = 100  # 序列长度
    step = 1.0 / L  # 时间步长 (秒)
    ks = np.arange(L)  # 时间索引
    
    # 生成输入力序列
    u = example_force(ks * step)  # 10Hz正弦波与阶跃函数的乘积

    # 运行状态空间模型仿真
    y = run_SSM(*ssm, u)  # 计算系统响应

    # 创建动画可视化
    import matplotlib.pyplot as plt
    from celluloid import Camera

    plt.style.use('default')
    
    # 创建3个子图
    fig, (ax1, ax2, ax3) = plt.subplots(3, figsize=(10, 8))
    camera = Camera(fig)
    
    # 设置子图标题
    ax1.set_title("输入力 $u_k$ (红色)")
    ax2.set_title("位置响应 $y_k$ (蓝色)")
    ax3.set_title("物体位置可视化")
    
    # 隐藏x轴刻度以避免重叠
    ax1.set_xticks([])
    ax2.set_xticks([])

    # 生成动画帧
    print("正在生成动画帧...")
    for k in range(0, L, 2):  # 每2个时间步生成一帧
        # 绘制累积的力和位置曲线
        ax1.plot(ks[:k], u[:k], color="red", linewidth=2)
        ax2.plot(ks[:k], y[:k], color="blue", linewidth=2)
        
        # 使用箱线图可视化物体当前位置
        # 创建一个表示物体边界的箱线图
        ax3.boxplot(
            [[y[k, 0] - 0.04, y[k, 0], y[k, 0] + 0.04]],  # 物体的上下边界
            showcaps=False,    # 不显示端盖
            whis=False,        # 不显示须线
            vert=False,        # 水平方向
            widths=10,         # 箱体宽度
        )
        
        # 设置y轴范围以保持可视化稳定
        ax3.set_ylim(-0.1, 0.1)
        
        # 拍摄当前帧
        camera.snap()

    # 创建动画
    print("正在创建动画...")
    anim = camera.animate(interval=100)  # 每100ms更新一帧
    
    # 保存动画为GIF文件
    print("正在保存动画文件...")
    anim.save("Mamba/image/line.gif", dpi=150, writer="pillow")
    print("动画文件保存完成！")
    
    # 打印仿真结果统计
    print(f"\n仿真结果统计:")
    print(f"最终位置: {y[-1, 0]:.4f}")
    print(f"最大位置: {np.max(y[:, 0]):.4f}")
    print(f"最小位置: {np.min(y[:, 0]):.4f}")
    print(f"位置变化范围: {np.max(y[:, 0]) - np.min(y[:, 0]):.4f}")

if __name__ == "__main__":
    """
    主程序入口
    运行状态空间模型示例并生成动画
    """
    print("=" * 50)
    print("Mamba状态空间模型(SSM)仿真")
    print("=" * 50)
    print("系统参数:")
    print("- 弹簧常数 k = 40 N/m")
    print("- 阻尼系数 b = 5 N·s/m") 
    print("- 质量 m = 1 kg")
    print("- 输入: 10Hz正弦波与阶跃函数")
    print("=" * 50)
    
    example_ssm()

可视化图像

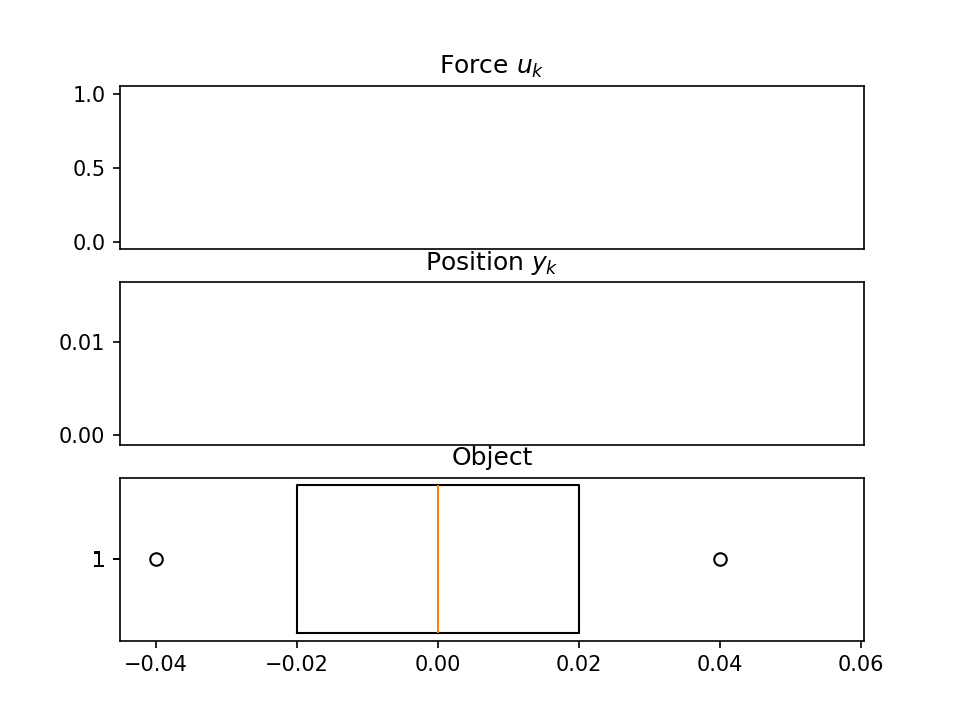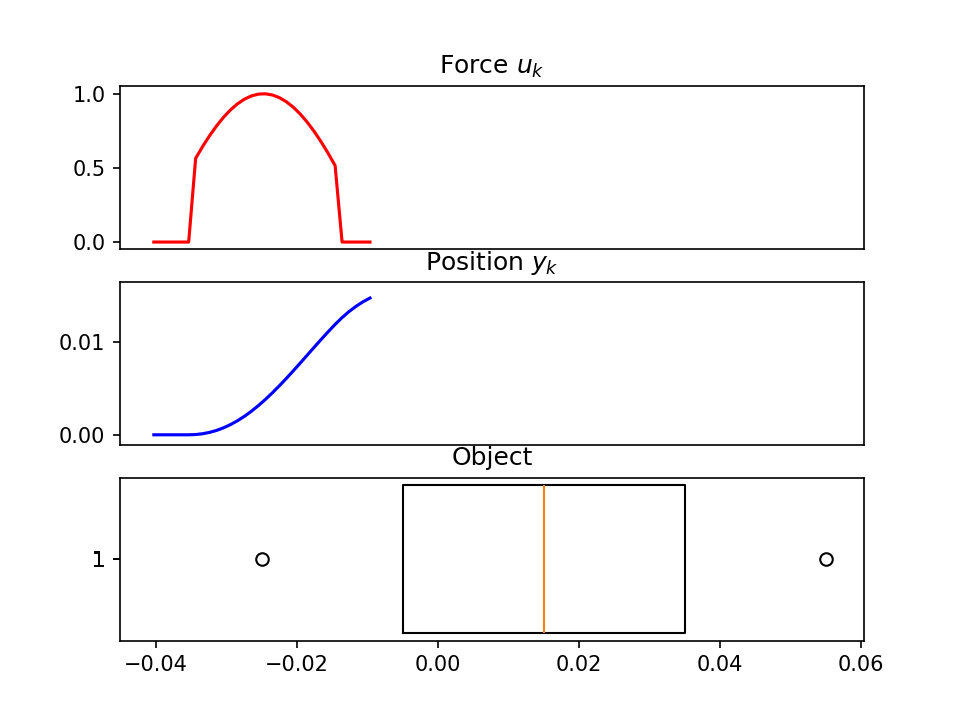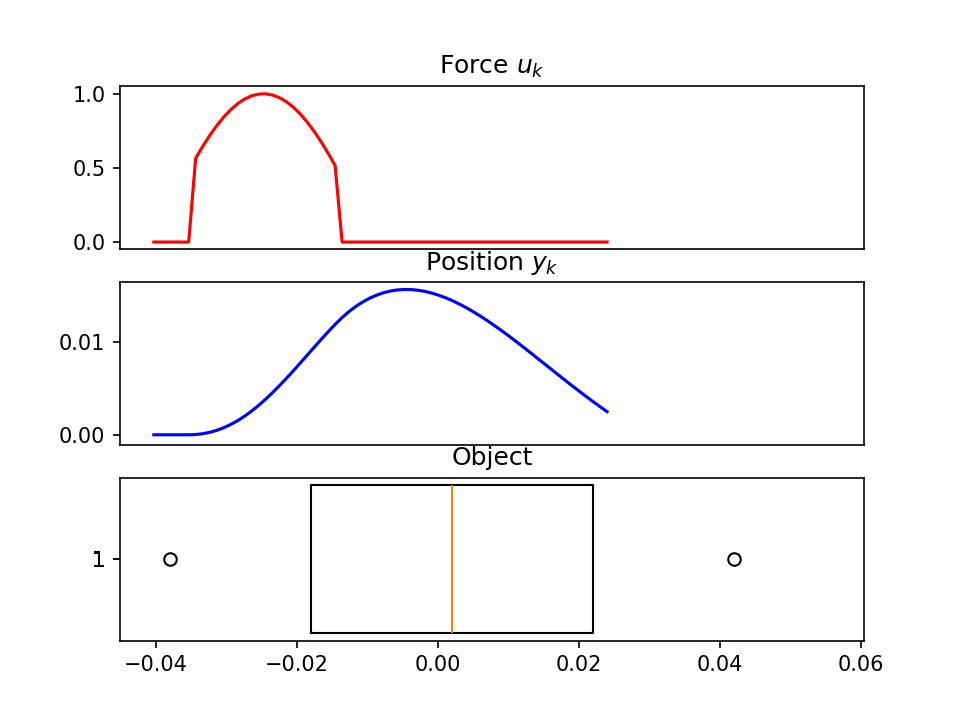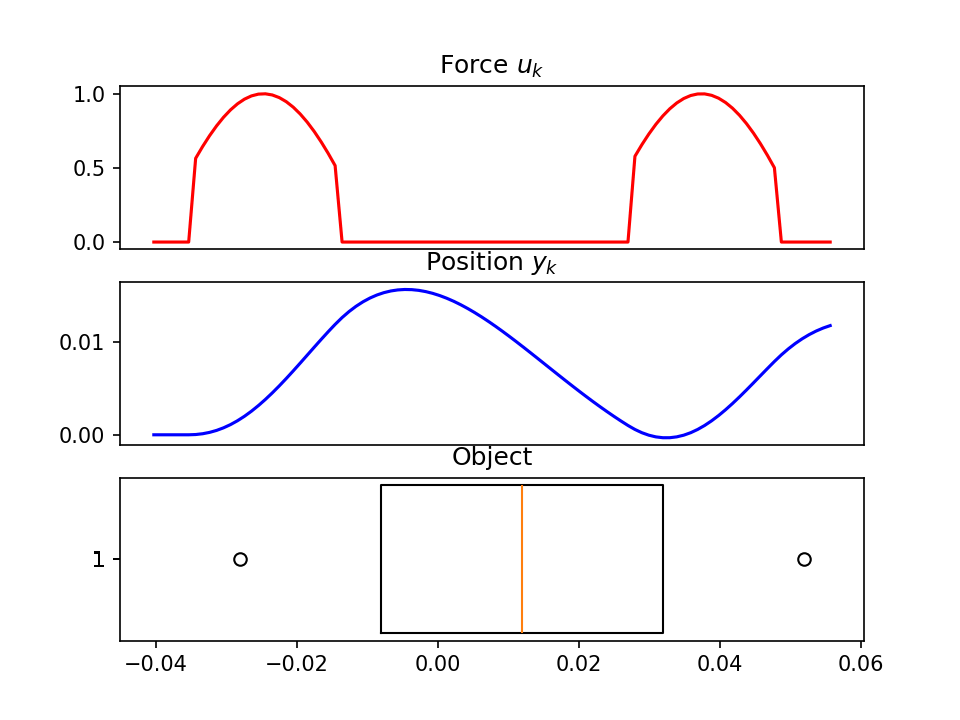
四、致谢

由于本人水平有限，对Mamba的理解可能有失偏颇，希望各位小伙伴能够积极指出！