Python SciPy 插值方法详解：数学原理与可视化案例

在科学计算与数据分析中，插值（Interpolation） 是一类重要的工具，用来在已知数据点之间推测未知点的函数值。SciPy 提供了丰富的插值函数接口，可以轻松实现从一维到多维的插值运算。本文将结合数学公式、SciPy 函数与 Python 可视化案例，系统梳理常见插值方法。

---

1. 一维插值方法详解与对比

1.1 构造一维数据集

我们选用目标函数
$$f(x)=\sin (x)+0.2\cos (3x)$$
并在区间 $[0,10]$ 内采样稀疏点，并加入少量高斯噪声，模拟实际实验数据或测量误差。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

sns.set_theme(style="whitegrid", font="SimHei", rc={"axes.unicode_minus": False})

# 定义目标函数
def f(x):
    return np.sin(x) + 0.2*np.cos(3*x)

# 构造稀疏数据点 + 噪声
np.random.seed(42)
x = np.linspace(0, 10, 10)
y = f(x) + 0.1*np.random.randn(len(x))

# 高密度采样用于可视化
x_true = np.linspace(0, 10, 400)
y_true = f(x_true)

plt.figure(figsize=(8,4))
plt.plot(x_true, y_true, "k--", label="真实函数 f(x)")
plt.scatter(x, y, color="red", label="原始数据点")
plt.legend()
plt.title("测试数据")
plt.show()

---

1.2 多项式插值（Polynomial Interpolation）

数学原理：
给定 $n+1$ 个数据点 $(x_i,y_i)$，多项式插值通过构造一个 $n$ 次多项式 $P(x)$，使其在每个已知数据点处精确拟合：
$$P(x_i)=y_i,i=0,1,\dots ,n$$
常用的形式为 Lagrange 插值：
$$P(x)=\sum _{i=0}^n{y}_i\prod _{\begin{array}{c}j=0\\ j\ne i\end{array}}^n\frac{x-x_j}{x_i-x_j}$$

Python 示例：

from scipy.interpolate import lagrange

poly = lagrange(x, y)
y_poly = poly(x_true)

plt.figure(figsize=(8,4))
plt.plot(x_true, y_true, "k--")
plt.scatter(x, y, color="red")
plt.plot(x_true, y_poly, "b", label="Lagrange 插值")
plt.legend()
plt.title("多项式插值：振荡现象明显")
plt.show()

特点：公式直观，易于理解。但在数据点较多时，容易出现 龙格现象，即高次多项式在区间边缘振荡。

---

1.3 样条插值（Cubic Spline Interpolation）

数学原理：
条插值在每个区间 $[x_i,x_{i+1}]$ 上构造三次多项式 $S_i(x)$，保证函数值、导数和二阶导数在节点连续：
$$S(x_i)=y_i,S(x_{i+1})=y_{i+1},S_i^{\prime }(x_{i+1})=S_{i+1}^{\prime }(x_{i+1})$$

Python 示例：

from scipy.interpolate import CubicSpline

cs = CubicSpline(x, y)
y_cs = cs(x_true)

plt.figure(figsize=(8,4))
plt.plot(x_true, y_true, "k--")
plt.scatter(x, y, color="red")
plt.plot(x_true, y_cs, "g", label="Cubic Spline")
plt.legend()
plt.title("三次样条插值：平滑性强")
plt.show()

特点：平滑性好，适合工程与科学计算中的连续曲线拟合。

---

1.4 B 样条插值（B-Spline Interpolation）

数学原理：
B 样条由基函数 $B_{i,k}(x)$ 线性组合而成：
$$S(x)=\sum _i{c}_i{B}_{i,k}(x)$$
可通过调整阶数 $k$ 与系数 $c_i$ 控制光滑度，适合大规模数据处理。

Python 示例：

from scipy.interpolate import make_interp_spline

spl = make_interp_spline(x, y, k=3)
y_bs = spl(x_true)

plt.figure(figsize=(8,4))
plt.plot(x_true, y_true, "k--")
plt.scatter(x, y, color="red")
plt.plot(x_true, y_bs, "purple", label="B-Spline")
plt.legend()
plt.title("B 样条插值：可调节平滑度")
plt.show()

特点：灵活性强，适合大规模数据，可控制光滑程度。

---

1.5 一维插值（interp1d）

数学原理：
$$f(x)=y_i+\frac{y_{i+1}-y_i}{x_{i+1}-x_i}(x-x_i),x\in [x_i,x_{i+1}]$$
scipy.interpolate.interp1d 提供快速一维插值接口，支持 linear、quadratic、cubic 等多种方法。

Python 示例：

from scipy.interpolate import interp1d

f_lin = interp1d(x, y, kind="linear")
f_cub = interp1d(x, y, kind="cubic")

plt.figure(figsize=(8,4))
plt.plot(x_true, y_true, "k--")
plt.scatter(x, y, color="red")
plt.plot(x_true, f_lin(x_true), "g", label="线性插值")
plt.plot(x_true, f_cub(x_true), "b", label="三次插值")
plt.legend()
plt.title("interp1d 插值对比")
plt.show()

特点：调用简单，适合快速实验和工程应用。

---

1.6 径向基函数插值（Radial Basis Function Interpolation, RBF）

数学原理：
$$s(x)=\sum _{i=1}^N{\lambda }_i,\varphi (|x-x_i|)$$
常见基函数：

• 高斯函数 $\varphi (r)=e^{-(ϵr{)}^2}$
• 多项式 $\varphi (r)=r^3$

Python 示例：

from scipy.interpolate import Rbf

rbf = Rbf(x, y, function="gaussian")
y_rbf = rbf(x_true)

plt.figure(figsize=(8,4))
plt.plot(x_true, y_true, "k--")
plt.scatter(x, y, color="red")
plt.plot(x_true, y_rbf, "brown", label="RBF")
plt.legend()
plt.title("径向基函数插值：拟合灵活")
plt.show()

特点：适合高维数据，灵活性强，但计算开销大。

---

1.7 Akima 插值

数学原理：
Akima 插值是一种分段三次插值方法，通过局部斜率计算每个区间的导数，从而抑制异常振荡，保证单调性和平滑性。
设一维数据点为 $(x_i,y_i)$，首先计算每段相邻点的斜率：
$$m_i=\frac{y_{i+1}-y_i}{x_{i+1}-x_i},i=0,1,\dots ,n-1$$
然后在每个节点 $x_i$ 处确定导数 $d_i$：
$$d_i=\frac{|m_{i+1}-m_i|m_{i-1}+|m_{i-1}-m_{i-2}|m_i}{|m_{i+1}-m_i|+|m_{i-1}-m_{i-2}|},i=2,\dots ,n-2$$
对边界点使用 外推法：

• 对第 0、1 个节点，通过线性外推计算导数：
  $$d_0=2m_0-d_1,d_1=2m_1-d_2$$
• 对最后两个节点 $x_{n-1},x_n$：
  $$d_{n-1}=2m_{n-2}-d_{n-2},d_n=2m_{n-1}-d_{n-1}$$
  区间三次多项式： 最后在每个区间构造三次多项式：
  $$S_i(x)=a_i+b_i(x-x_i)+c_i(x-x_i{)}^2+d_i(x-x_i{)}^3,x\in [x_i,x_{i+1}]$$
  其中系数由节点值 $y_i$ 与导数 $d_i$ 确定。

Python 示例：

from scipy.interpolate import Akima1DInterpolator

akima = Akima1DInterpolator(x, y)
y_akima = akima(x_true)

plt.figure(figsize=(8,4))
plt.plot(x_true, y_true, "k--")
plt.scatter(x, y, color="red")
plt.plot(x_true, y_akima, "teal", label="Akima 插值")
plt.legend()
plt.title("Akima 插值：局部单调性更好")
plt.show()

特点：在数据变化剧烈时比样条更稳健，避免异常振荡。

---

2. 二维插值方法详解与对比

2.1 构造二维数据集

我们考虑二维目标函数：
$$f(x,y)=\sin (3x)\cos (3y)$$
在 $[0,1]\times [0,1]$ 内随机采样 100 个点并加入噪声，作为测试数据。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

sns.set_theme(style="whitegrid", font="SimHei", rc={"axes.unicode_minus": False})

# 构造二维函数 + 噪声
np.random.seed(42)
points = np.random.rand(100, 2)  # 随机点 (x,y)
values = np.sin(3*points[:,0]) * np.cos(3*points[:,1]) + 0.1*np.random.randn(100)

# 构造网格用于插值
grid_x, grid_y = np.mgrid[0:1:200j, 0:1:200j]

plt.figure(figsize=(6,5))
plt.scatter(points[:,0], points[:,1], c=values, cmap="viridis", edgecolor="k")
plt.title("二维随机采样点")
plt.colorbar(label="f(x,y)")
plt.show()

---

2.2 最近邻插值（Nearest Interpolation）

数学原理：
最近邻插值选择距离目标点最近的已知数据点的函数值：
$$f(x,y)=f(x_i,y_i),(x_i,y_i)=\arg \underset{(x_j,y_j)}{\min }\sqrt{(x-x_j{)}^2+(y-y_j{)}^2}$$

Python 示例：

from scipy.interpolate import griddata

grid_z_nearest = griddata(points, values, (grid_x, grid_y), method="nearest")

plt.figure(figsize=(6,5))
plt.imshow(grid_z_nearest.T, extent=(0,1,0,1), origin="lower", cmap="viridis")
plt.scatter(points[:,0], points[:,1], c=values, edgecolor="k", s=20, cmap="viridis")
plt.title("Nearest 插值")
plt.colorbar()
plt.show()

特点：简单快速，但结果呈块状，不连续。

---

2.3 线性插值（Linear Interpolation）

数学原理：
在每个三角剖分单元内，使用平面函数插值：
$$f(x,y)=a+bx+cy$$

Python 示例：

from scipy.interpolate import griddata

grid_z_linear = griddata(points, values, (grid_x, grid_y), method="linear")

plt.figure(figsize=(6,5))
plt.imshow(grid_z_linear.T, extent=(0,1,0,1), origin="lower", cmap="viridis")
plt.scatter(points[:,0], points[:,1], c=values, edgecolor="k", s=20, cmap="viridis")
plt.title("Linear 插值")
plt.colorbar()
plt.show()

特点：计算速度快，连续但不一定光滑。

---

2.4 三次插值（Cubic Interpolation）

数学原理：
Cubic 插值通过二维三次样条函数，保证函数值及一阶导数连续。对每个单元可以写作：
$$f(x,y)=\sum _{i=0}^3\sum _{j=0}^3{a}_{ij}{x}^i{y}^j$$
其中系数 $a_{ij}$ 由周围节点函数值拟合确定。

Python 示例：

from scipy.interpolate import griddata

grid_z_cubic = griddata(points, values, (grid_x, grid_y), method="cubic")

plt.figure(figsize=(6,5))
plt.imshow(grid_z_cubic.T, extent=(0,1,0,1), origin="lower", cmap="viridis")
plt.scatter(points[:,0], points[:,1], c=values, edgecolor="k", s=20, cmap="viridis")
plt.title("Cubic 插值")
plt.colorbar()
plt.show()

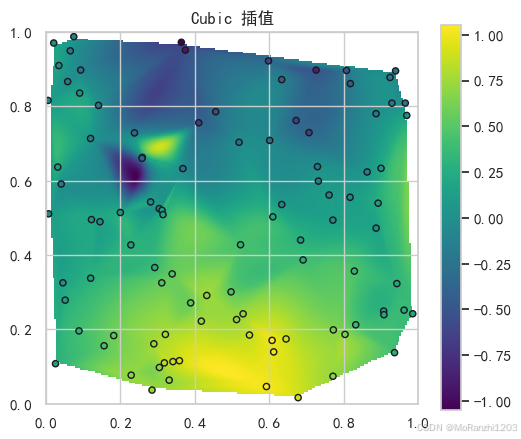
特点：生成平滑曲面，但在稀疏区域可能出现拟合失真。

---

2.5 径向基函数插值（RBF Interpolation）

数学原理：
RBF 插值将函数表示为以各数据点为中心的径向基函数加权和：
$$s(x,y)=\sum _{i=1}^N{w}_i,\varphi \left(\sqrt{(x-x_i{)}^2+(y-y_i{)}^2}\right)$$
其中 $\varphi (r)$ 是基函数，如高斯函数 $\varphi (r)=e^{-(ϵr{)}^2}$，权重 $w_i$ 由已知数据点确定。

Python 示例：

from scipy.interpolate import RBFInterpolator

rbf = RBFInterpolator(points, values, kernel="gaussian", epsilon=0.1)
xy_grid = np.column_stack([grid_x.ravel(), grid_y.ravel()])
grid_z_rbf = rbf(xy_grid).reshape(grid_x.shape)

plt.figure(figsize=(6,5))
plt.imshow(grid_z_rbf.T, extent=(0,1,0,1), origin="lower", cmap="viridis")
plt.scatter(points[:,0], points[:,1], c=values, edgecolor="k", s=20)
plt.title("RBF 插值 (Gaussian)")
plt.colorbar()
plt.show()

特点：适合任意分布的散点数据拟合，结果平滑，但计算开销大。

---

3. 总结

本文系统梳理了 SciPy 中常用的一维与二维插值方法，并结合数学公式与 Python 可视化示例，帮助理解各类插值方法的原理与适用场景。在一维插值方面，从简单的 多项式插值（Lagrange） 到平滑性更好的 三次样条（Cubic Spline） 与 B 样条（B-Spline），再到灵活稳健的 Akima 插值 与高维适用的 径向基函数插值（RBF），每种方法在精度、平滑性和计算复杂度上各有优劣：

1. 多项式插值公式简单直观，但在节点较多时容易出现高次振荡（龙格现象）。
2. 样条插值通过保证一阶、二阶导数连续，实现平滑曲线拟合，适合工程和科学计算。
3. B 样条插值通过基函数线性组合，可以调节光滑度与拟合灵活性，适合大规模数据。
4. interp1d 提供快速一维插值接口，支持线性、二次、三次等多种方法，便于快速实验。
5. Akima 插值通过局部斜率加权计算导数，能够在数据剧烈变化时避免异常振荡，保证单调性和局部平滑。
6. 径向基函数插值（RBF） 适合高维和不规则散点数据，拟合灵活，但计算量较大。

在二维插值方面，常用方法包括 最近邻插值、线性插值、三次插值 和 RBF 插值：

1. 最近邻插值计算简单，但结果块状、不连续。
2. 线性插值保证连续性，速度快，适合网格化数据。
3. 三次插值生成平滑曲面，但稀疏区域可能拟合失真。
4. 二维 RBF 插值适合任意散点数据，结果平滑，但计算成本高。

总的来说，选择插值方法应根据 数据特性、平滑性要求、计算成本 和 是否需要处理高维或稀疏数据 来决定。本文提供的数学公式和可视化示例，可作为实际工程与科学计算中 插值方法选择与调试 的参考指南。