一、背景介绍

        在数据分析和机器学习领域，线性回归是一种广泛应用的算法，用于研究变量之间的线性关系。本文将通过一个具体的案例，展示如何使用 Python 的相关库（如 Pandas、Matplotlib、Scikit-learn 等）来实现线性回归模型的构建、训练、预测以及评估。

        这是本人在课上按照老师要求敲的一个代码实验，希望对刚接触机器学习和数据分析的同志有所帮助。

二、数据预处理

        首先，我们需要读取存储在 CSV 文件中的电影数据，并使用 Pandas 库将其转换为 DataFrame 格式，以便于后续的数据操作和分析。

通过网盘分享的文件：3_film.csv
链接: https://pan.baidu.com/s/1t2_FkttEbrn3sRB-lIKr6Q?pwd=1111 提取码: 1111

import pandas as pd

df = pd.read_csv('3_film.csv') # 读取 csv 数据
df.head() # 展示前五行数据，了解数据结构

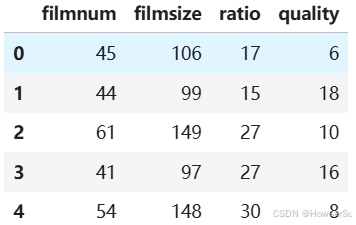
         为了初步了解数据的分布情况，我们绘制了直方图。直方图可以直观地展示每个特征值的频数分布，帮助我们判断数据是否符合正态分布等统计特性。

import matplotlib.pyplot as plt

plt.figure(figsize=(15, 8)) # 设置图片尺寸
df.hist() # 绘制直方图
plt.show()

df.hist(xlabelsize=12, ylabelsize=12, figsize=(12, 7)) # 调整直方图尺寸
plt.show()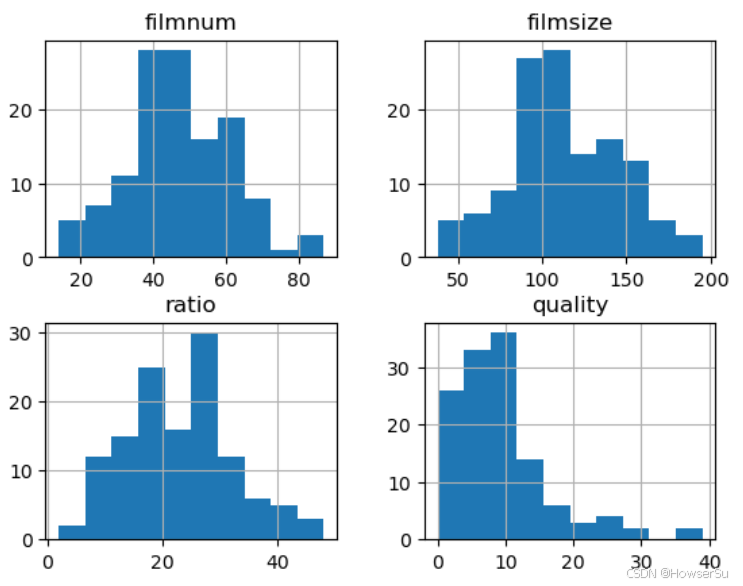

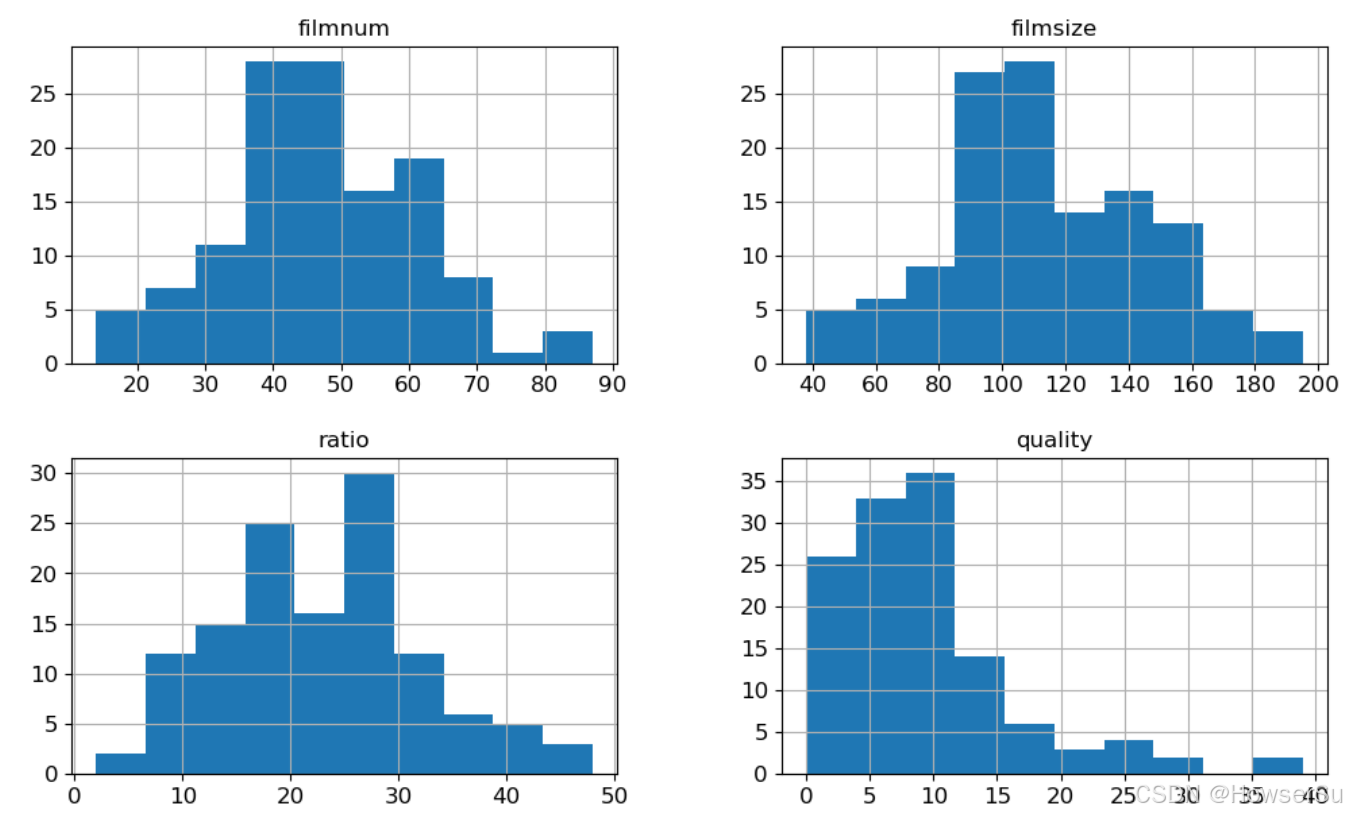
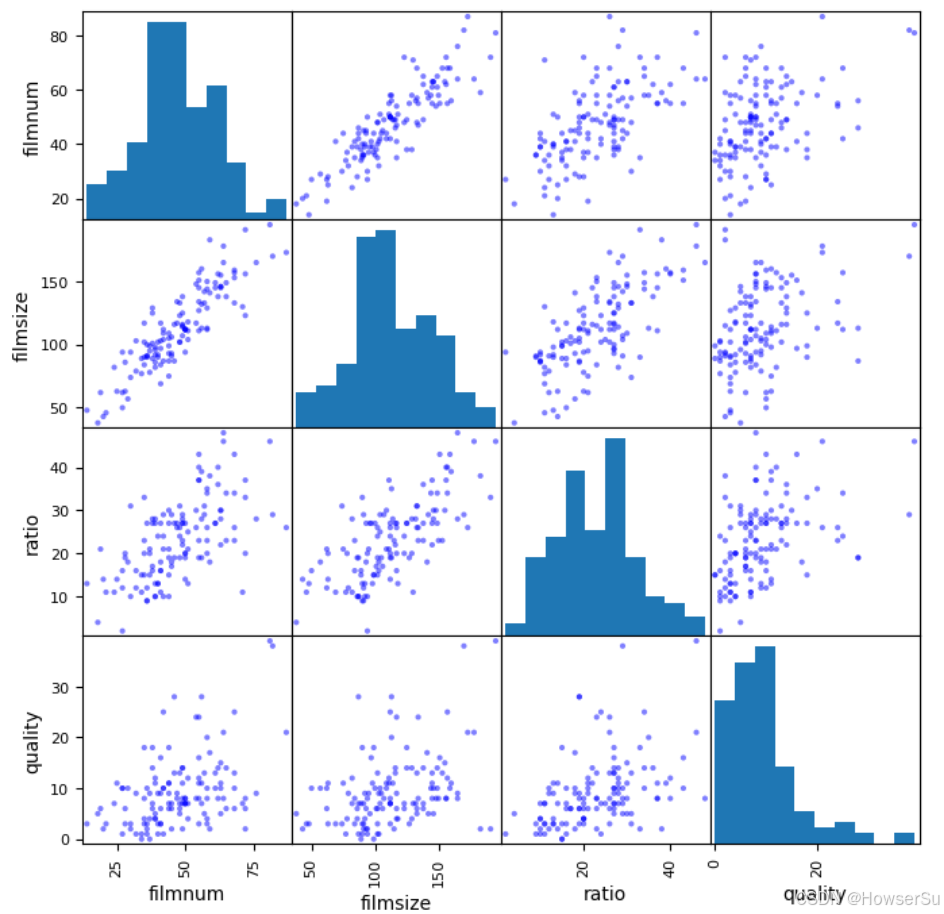
         进一步地，我们使用散点图矩阵来观察不同特征之间以及特征与目标变量之间的关系。散点图矩阵可以一次性展示多个变量之间的两两关系，有助于发现潜在的线性或非线性关联。

from pandas.plotting import scatter_matrix

scatter_matrix(df, figsize=(8, 8), c='b') # 绘制散点图矩阵
plt.show()

三、模型构建与训练

        在数据预处理完成后，我们需要将数据集划分为训练集和测试集。这里我们选择将 75% 的数据作为训练集，25% 的数据作为测试集，以确保模型在训练过程中有足够的数据学习模式，同时保留一部分数据用于评估模型的泛化能力。

from sklearn.model_selection import train_test_split

X = df.iloc[:, 1:4] # 选取特征变量
y = df.filmnum # 设定目标变量为 y

# 把 X、y 转换为数组形式，以便于计算
X = np.array(X.values)
y = np.array(y.values)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=1)

         接下来，我们使用 Scikit-learn 库中的 LinearRegression 模块来构建线性回归模型，并利用训练集对模型进行训练，求解模型的参数（截距项和系数）。

from sklearn.linear_model import LinearRegression

lr = LinearRegression() # 设定回归算法
lr.fit(X_train, y_train) # 使用训练数据进行参数求解

print('求解截距项为：', lr.intercept_)
print('求解系数为：', lr.coef_)

四、模型预测与结果评估

        训练好的模型需要在测试集上进行预测，以评估其性能和泛化能力。我们使用均方误差（MSE）、均方根误差（RMSE）和平均绝对误差（MAE）等指标来量化模型的预测误差，同时计算决定系数（R²）来衡量模型对数据的拟合优度。

y_hat = lr.predict(X_test) # 对测试集进行预测

# 绘制实际值与预测值的对比图
plt.figure(figsize=(10, 6))
t = np.arange(len(X_test))
plt.plot(t, y_test, 'r', linewidth=2, label='y_test')
plt.plot(t, y_hat, 'g', linewidth=2, label='y_hat')
plt.legend()
plt.show()

from sklearn import metrics
from sklearn.metrics import r2_score
import numpy as np

# 输出模型评估指标
print("r2:", lr.score(X_test, y_test))
print("r2_score:", r2_score(y_test, y_hat))
print("MAE:", metrics.mean_absolute_error(y_test, y_hat))
print("MSE:", metrics.mean_squared_error(y_test, y_hat))
print("RMSE:", np.sqrt(metrics.mean_squared_error(y_test, y_hat)))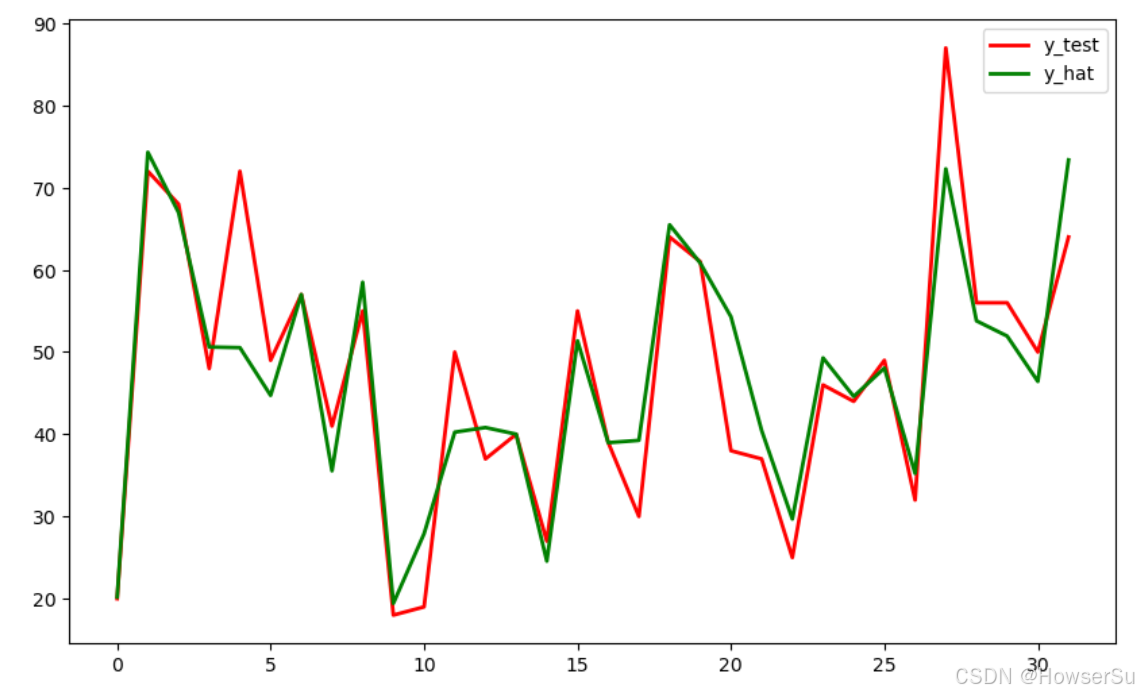

五、结果分析

        根据运行结果，我们得到以下模型评估指标：

 r2: 0.8279404383777595
r2_score: 0.8279404383777595
MAE: 4.63125112009528
MSE: 46.63822281456598
RMSE: 6.8292183165107545

        从结果来看，决定系数 R² 接近 1，表明模型对数据的拟合效果较好，能够解释大部分的变异。均方误差 MSE 和均方根误差 RMSE 的值相对较小，说明模型的预测值与实际值之间的平均误差在可接受范围内。平均绝对误差 MAE 也进一步验证了模型的预测精度。

六、总结

        通过本次实践，我们成功地使用 Python 实现了线性回归模型的构建、训练、预测和评估。从数据预处理到模型结果分析，每一步都至关重要。线性回归作为一种基础的机器学习算法，在处理具有线性关系的数据时表现出色。然而，在面对更复杂的数据关系时，可能需要考虑其他更高级的算法或对数据进行进一步的处理和特征工程。