这个栗子解释的是 怎么引用特征值越大包含信息量越多这一特性来 进行降维。

问题的引入

机器学习中的分类问题，给出178个葡萄酒样本，每个样本含有13个参数，比如酒精度、酸度、镁含量等，这些样本属于3个不同种类的葡萄酒。任务是提取3种葡萄酒的特征，以便下一次给出一个新的葡萄酒样本的时候，能根据已有数据判断出新样本是哪—种葡萄酒。
问题详细描述:UCI Machine Learning Repository: Wine Data Set
训练样本数据:archive.ics.uci.edu/ml/ …

解决

原数据有13维，但这之中含有冗余，减少数据量最直接的方法就是降维。
做法:把数据集赋给一个178行13列的矩阵R，减掉均值并归一化，它的协方差矩阵$C=R^{T}R$，C是13行13列的矩阵，对C进行特征分解，对角化$C=UD{U}^T$，其中U是特征向量组成的矩阵，D是特征之组成的对角矩阵，并按由大到小排列。然后，另$R‘=RU$，就实现了数据集在特征向量这组正交基上的投影。嗯，重点来了，$R’$中的数据列是按照对应特征值的大小排列的，后面的列对应小特征值，去掉以后对整个数据集的影响比较小。比如，现在我们直接去掉后面的7列，只保留前6列，就完成了降维。这个降维方法叫PCA(Principal Component Analysis)。下面看结果: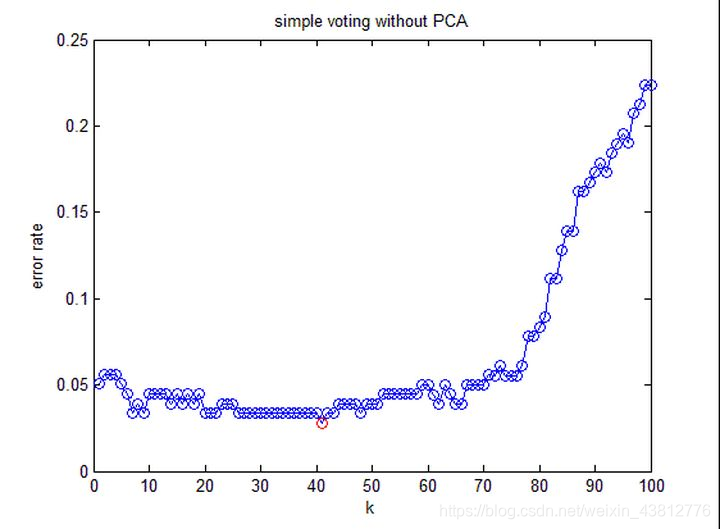

这是不降维时候的分类错误率。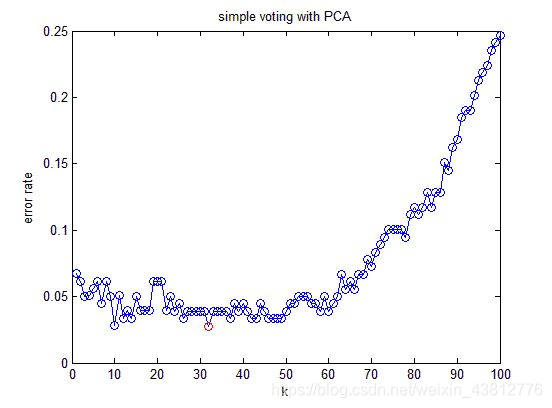

这是降维以后的分类错误率。

END

结论:降维以后分类错误率与不降维的方法相差无几，但需要处理的数据量减小了一半(不降维需要处理13维，降维后只需要处理6维)。