数据挖掘笔记 - 数学基础(卷积)
一、初识卷积卷积之所以叫“卷”积,可以参见知乎上的回答。个人认为,卷积的通俗理解就是“长江后浪推前浪,前浪死在沙滩上”。“后浪”推“前浪”的本质就是“后浪”和“前浪”叠加,然而随着时间推移,“前浪”并不会因为“后浪们”的叠加的“推”而越来越大,因为“浪”的势头会随着时间推移慢慢消解,最终导致“前浪死在沙滩上”而不是造成大“江”啸。卷积函数就是所有位置的“浪”的高低。关于卷积,我主要参考了几...
一、初识卷积
卷积之所以叫“卷”积,可以参见知乎上的回答。个人认为,卷积的通俗理解就是“长江后浪推前浪,前浪死在沙滩上”。“后浪”推“前浪”的本质就是“后浪”和“前浪”叠加,然而随着时间推移,“前浪”并不会因为“后浪们”的叠加的“推”而越来越大,因为“浪”的势头会随着时间推移慢慢消解,最终导致“前浪死在沙滩上”而不是造成大“江”啸。卷积函数就是所有位置的“浪”的高低。
关于卷积,我主要参考了几篇相关文章:
二、卷积的基本定义及应用
卷积的定义:
设函数和
是定义在
上的两个可积函数,那么如下反常积分成为
与
的卷积,记做
:
其离散形式为:
在信号学里,卷积的物理意义可以解释为在时间点接收到的信息总量,其中函数
是信号发射函数,和
是信号随时间衰减的函数,而变量
则是发射信号的时间点。如果信号是连续发射的,则适用连续形式,如果信号是间断的(脉冲信号),则适用离散形式。
在统计学里,卷积可以表现为关于时间的移动加权平均函数,其中函数
是时间点
上的统计对象的值,和
是统计对象历史值的权重。
一维卷积可以拓展为二维卷积:
设函数和
是定义在
上的两个可积函数,那么
与
的卷积如下所示:
其离散形式为:
二维卷积经常应用在图像处理中,其中函数和
分别是用来读取两个矩阵(目前设为
和
)中
行
列的值,
其实就是矩阵
中的所有点。那么二维卷积的离散形式可以理解为分别吧矩阵
中的所有点和矩阵
中对应的点相乘(这是元素级的运算)并求和(矩阵所有元素求和)。这种操作可以用来对图像中的每一个点进行相关处理(就是二维的加权移动平均)。
举个具体例子,假设有图像(矩阵),平滑算子矩阵
,其中:
设函数为读取矩阵
中
行
列的值,比如
;
为读取矩阵
中
行
列的值,比如
(这里这么设置一个平移量是为了方便在卷积公式中计算)。
那么卷积可以表示为:
就是像素点及它周围一圈像素点的算术平均数。这里特别注意,在用矩阵
平滑像素点
时,从原矩阵
中抽取与矩阵
相同形状的子矩阵(红色区域)
:
然后通过对矩阵进行翻转(水平翻转+垂直翻转)得到矩阵
,再和子矩阵
计算哈达玛积(hadamard product)
,然后元素求和。
当使用二维卷积对整个图片进行处理的动态示意图如下(事实上超出原图矩阵范围的部分可用0补齐):
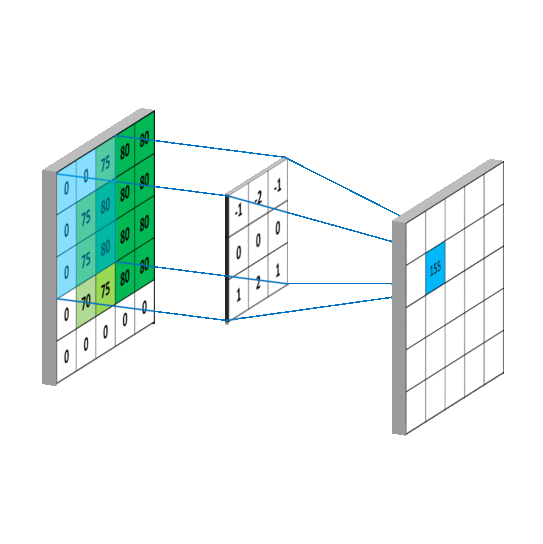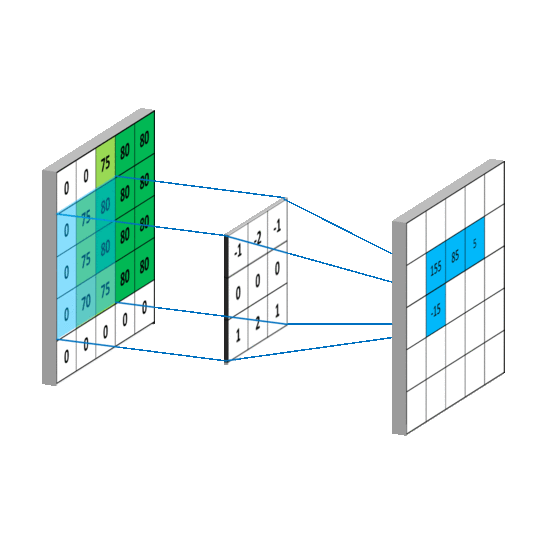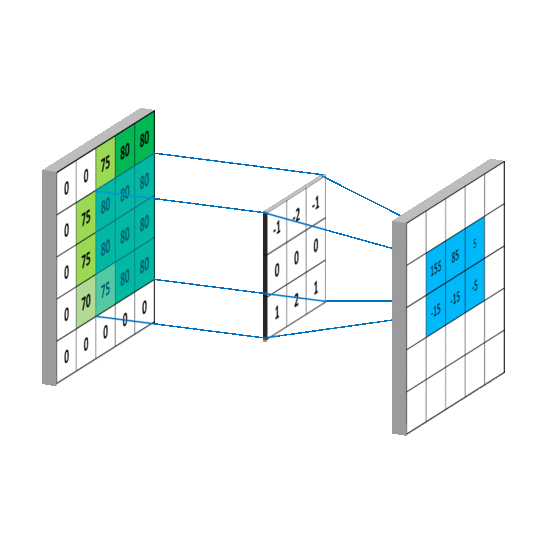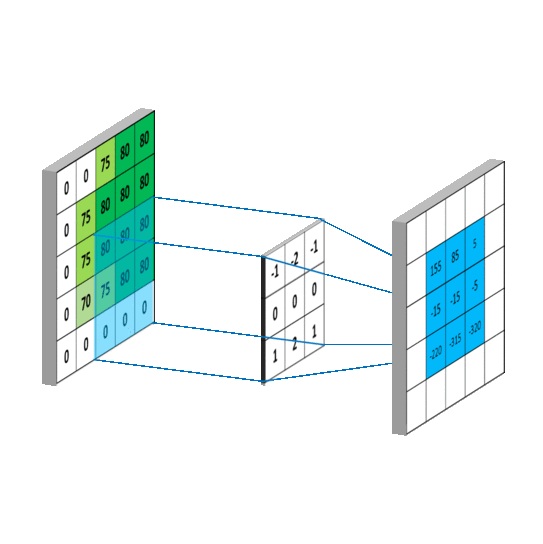
卷积在机器学习中,一个重要的作用就是处理特征工程,就像上面提到的图像处理(图像本身就是一个特征数据矩阵),卷积可以对数据矩阵进行“移动加权平均处理”,来“抹平”或者“突出”一些特征,其中用来进行“移动加权平均处理”的函数可以称为卷积核(本质就是核函数)。在数据可视化中,核密度图(KDE)本质也是对散点进行卷积计算,通过使用不同的卷积核函数来实现不同的核密度图。
三、卷积是如何“卷”的
卷积本身就是“低维度的”,因为各个维度之间被约束着,只是通过高纬度的被积函数去理解和计算。下面通过一个具体的例子来直观的看一下卷积的降维过程:
首先设两个函数和
,其中
,其中
是当前时间点,函数
是一个连续信号函数(这个信号每时每刻都在周期性地改变),
是信号发射时间点。函数
是一个信号衰减函数,
是距离信号发出时间点的时间间隔。
信号函数和衰减函数
函数图如下:
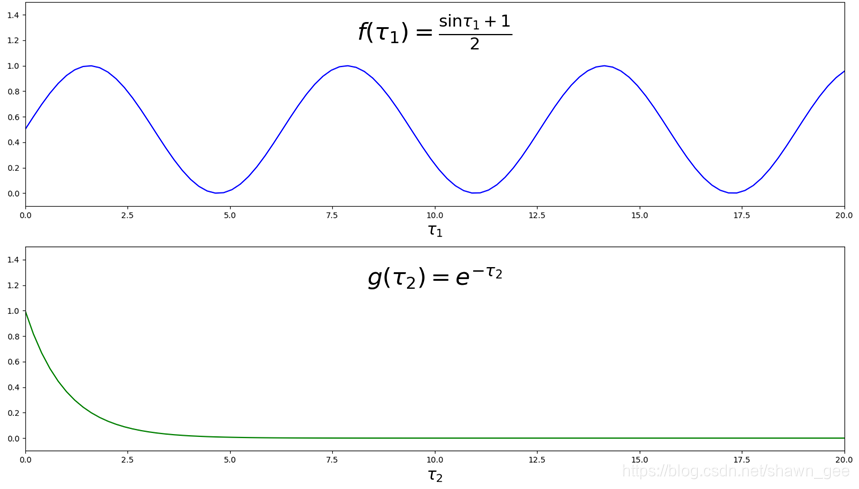
卷积如下所示:
其中被积函数就是两个函数值向量的张量积。之所以积分的上下限分别设置为
及
是因为:信号函数
在
时无意义(时间原点之前不发信号),衰减
在
时也无意义(当前时间之后收到的信号权重为0)。
卷积函数和被积函数
的函数图如下:
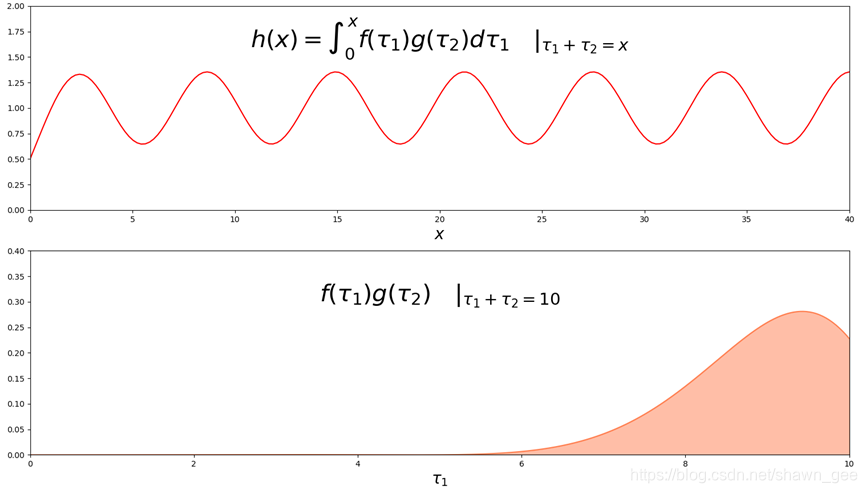
其中被积函数是在的条件下得到的一个关于
的一元函数(
被约束
所固定),
就等于橙色面积。
将以上4张图合并到一个三维空间中,各函数图颜色保持不变,蓝色曲线是函数,绿色曲线是函数
,红色曲线是卷积函数
,橙色曲线是函数
,网格就是整个完整的被积函数
曲面,橙色面就是经过直线
的垂直面截面,如下所示:
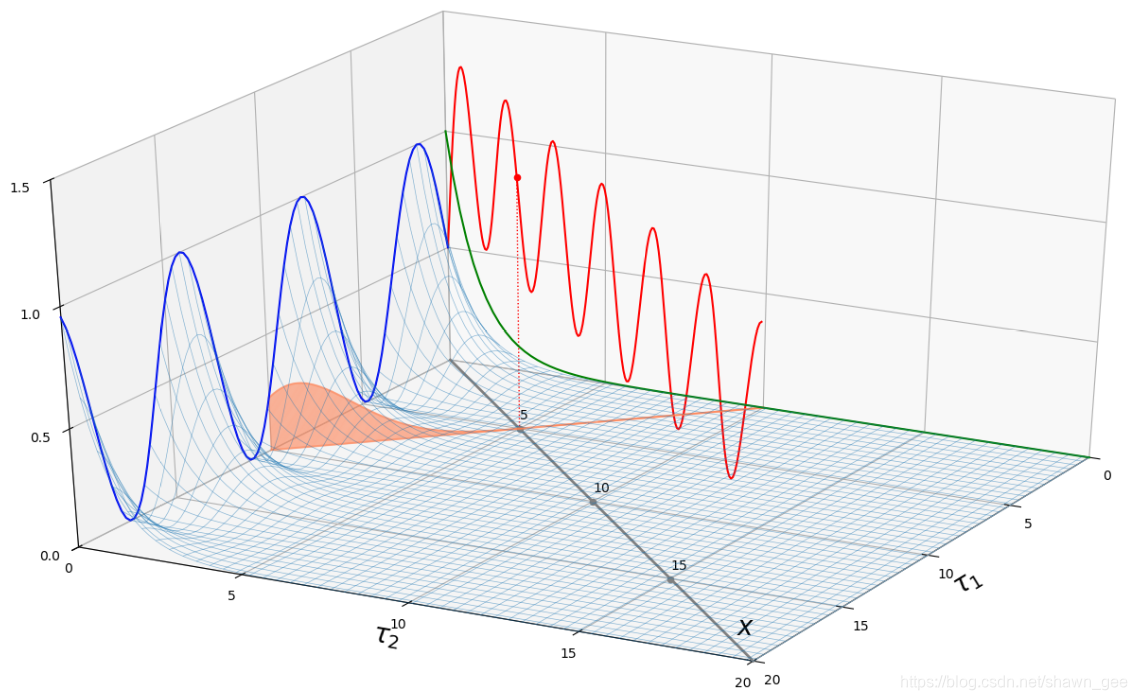
从上图可以看出卷积曲线就是由无数个垂直于直线的面去和被积函数曲面相交,并计算截面面积后所得到的。也就是说,整个三维空间沿着平面
的轨迹向原点方向压缩成了一个二维空间,整个过程中,除了
和
外的第三维度不变,维度
和
压缩成了
,就是上图的灰色直线(注意
轴的刻度和
轴刻度的关系),这就是三维空间中卷积的降维过程。
将上述过程拓展到大于三维的空间:将维空间中的被积函数沿着超平面
的方向,将无数个垂直经过
(
)的
维超平面和被积函数相交所得到的“超截面”的“超体积”“卷”成一个
维超曲面,之所以用卷而不是压,是因为整个过程连减两维(就像在三维空间中把一张布卷成一根绳子)。
卷积是一种“选择性”的降维,因为它没有用到被积函数的所有信息,只选择了平面
方向上的信息,整个被积函数沿着这个方向进行压缩。
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容








所有评论(0)