第三章 数据预处理

3.1 数据预处理：概述

​ 数据有可能是有缺失、不一致、有噪声、高维

• 数据质量：

  保证完整性 一致性 有噪声 准确性 时效性 可信性 可解释性

• 数据预处理的主要工作：

  • 抓取/抽取工作：从不同的网络、平台、 数据库、数据格式、 应用中抽取数据。

  • 清洗：空缺、噪声数据处理等

  • 集成数据：合并、汇总、过滤等

  • 降维：将高维数据降低到低维空间中

  • 转换：重新格式化和转换

    质量差$\to$数据清洗$\to$质量可控
    来源多样化$\to$数据集成$\to$统一数据
    维度灾难$\to$数据降维$\to$低维表示
    规范不统一$\to$数据转换$\to$规范化的数据

3.2 数据抽取

• 词频：

$$词频(TF)=某个词在文章中的出现次数$$

• “词频”进行标准化：

$$词频(TF)=\frac{某个词在文章中的出现次数}{文章的总词数}$$

• TF-IDF：
  $$逆文档频率(IDF)=log(\frac{语料库的文档总数}{包含该词的文档数+1})$$

  $$TF-IDF=词频(TF)\times 逆文档频率(IDF)$$

3.3 数据清洗

• 现实世界的数据一般为脏数据：许多潜在的不正确的数据，eg.仪器故障，人为或电脑错误，传输错误
  • 不完整：缺少属性值，缺少某些感兴趣的属性
  • 有噪声：包含噪声、误差或异常值
  • 不一致：包含代码或名称上的差异
  • 蓄意： 伪装缺失的数据
• 缺失值：
  • 数据丢失的原因：
    • 设备异常
    • 人为失误
    • 输入时，有些数据因得不到重视而没有被输入
    • 不适用(N/A)
  • 如何处理空缺值：
    • 忽略元组
    • 人工填写空缺值
    • 自动填充：
      • 使用一个全局变量填充空缺值：比如“unknown”或∞
      • 使用属性的平均值填充空缺值
      • 使用与给定元组属同一类的所有样本的平均值
      • 使用最可能的值填充空缺值(建模预测)
• 噪声数据：
  • 一个测量变量中的随机错误或偏差
  • 引起不正确属性值的原因：
    • 数据收集工具的问题
    • 数据输入错误
    • 数据传输错误
    • 技术限制
  • 如何处理噪声数据：
    • 分箱：
      • 按递增顺序对数据进行排序
      • 分到（等频的）箱子中
      • 使用光滑技术
        • 箱均值光滑
        • 箱中位数光滑
        • 箱边界光滑
  • 离群点不等于异常点
    • 处理离群点：
      • 聚类：将联系松散的数据当作离群点，监测并且去除离群点。 聚类集合之外的点即为离群点。
      • 回归：通过让数据适应回归函数来平滑数据（线性回归或非线性 回归）。
      • 盒图：通过盒图画出离群点

3.4 数据集成

• 将多个数据源中的数据合并，存放在一个数据存储中。如放在数据仓库中。
• 数据集成有助于减少结果数据集的冗余和不一致，提高挖掘过程的准确性和速度。

3.4.1 数据集成存在的问题

3.4.1.1实体识别问题

• 从多个数据源识别现实世界的实体。
• 利用元数据：每个属性的元数据包括名字、含义、数据类型和属性的值的允许范围，以及处理空缺值的规则。（元数据可以避免模式集成的错误，有助于变化数据）

3.4.1.2 属性冗余和相关性

• 同一属性在不同的数据库中会有不同的字段名；一个属性可以由另外的属性导出（“派生”属性），即两个属性是相关的。

1.标称数据的卡方检验

• 假设A有c个不同的值：a₁,a₂,a₃,$\cdots$,a_c B有r个不同的值：b₁,b₂,b₃,$\cdots$,b_r
• 包含属性A和属性B的元组可以使用一个相依表表示，其中A属性的c个不同值构成表的列，B属性的r个不同值构成表的行。
• 令(A_i,B_j)表示属性A取a_i而属性B取b_j的联合事件，即(A=a_i,B=b_j)。
• 标称数据的卡方相关检验

2.数值数据的相关系数

• 相关系数
• 通过计算x和y不存在线性相关关系，但实际可能会存在非线性相关的关系。

3.数值数据的协方差

• 相关性和协方差是评价两个属 性是否一起发生变化的两种相似的测量。
• 协方差
• 如果A和B相互独立（没有关联），则协方差为0。反过来并不成立。

3.4.1.3 元组重复

3.4.1.4 数据值冲突的检测与处理

3.5 数据归约：合并多个数据源

• 数据归约：用来获得数据集的归约表示
  • 属性个数更小
  • 对象数量更小
  • 但任然更接近于保持原始数据的完整性
  • 为什么进行数据归约？ 为了存储量和计算量

3.5.1 数据归约的概述

• 维归约：减少所考虑的随机变量或属性的个数。
  • 属性自己选择
  • 主成分分析
  • 扩展方法(LDA、NMF)
• 数量归约：用替代的、较小的数据表示形式替换原数据。
  • 回归模型：参数化数据归约
  • 直方图
  • 聚类
  • 抽样
• 数据归约的策略：
  • 维归约：通过删除不相干的属性(或维)，或者对属性进行重构
  • 数量规约：通过删除冗余的对象，减少数据量

3.5.2 属性子集选择

• 子集选择：

  • 目标：找出最小属性集，使得数据类别的分布尽可能接近使用所有属性的原始分布。

  • 好处：减少属性的数目，使得模式更易于理解。

  • 启发式的（探索性的/贪心算法）方法

    • 逐步向前选择：从空集开始，逐步添加

    • 逐步向后删除：从整个属性集开始，逐步删除

    • 向前选择和向后删除相结合

  • 属性子集选择标准

    • 信息增益(IG)：评价重要程度

  • 互信息(MI)

• 熵：描述数据的不确定性
  比较确定时，熵值较小；完全不确定时，熵值最大；完全确定时，熵值为0
  $$H(X)=-\sum _{i=1}^{n}p(x_i)lo{g}_{b}p(x_i)$$

  $$Gain(S,X)=H(S)-(H|X)$$

  信息增益IG；如果IG越大，说明消除不确定的程度越大。

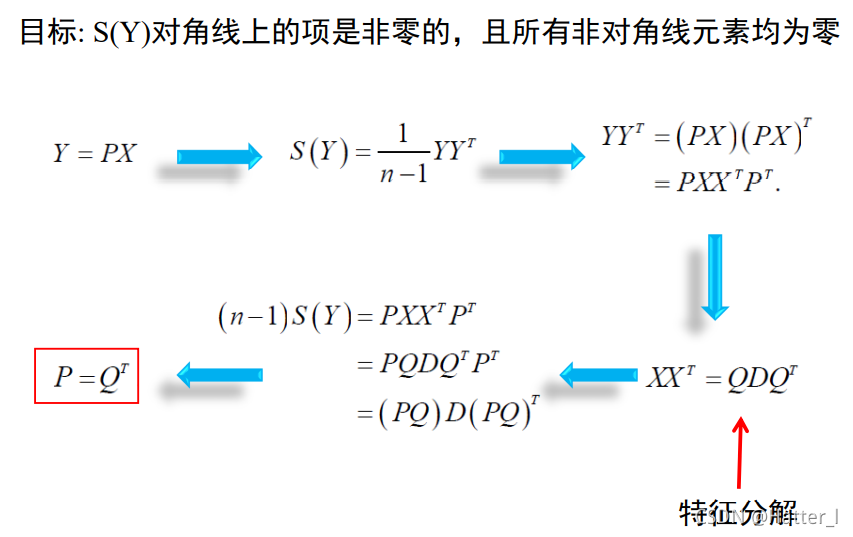
3.5.3 主成分分析

• 搜索k个最能代表数据的d维正交向量，其中k<=d
• 原数据投影到一个更小的空间上，导致维归约
• 目标是创建一个替换的、较小的变量集“组合”属性

3.5.4 扩展方法

• LDA主题模型(Latent Dirichlet Allocation)
  • 是Blei等人于2003年提出的基于概率模型的主题模型算法，LDA是一种非监督机器学习技术，可以用来识别大规模文档集或语料库中的潜在隐藏的主题信息。该方法假设每个词是由背后的一个潜在隐藏的主题中抽取出来。
• 非负矩阵分解NMF(Nonnegative Matrix Factorization)

3.5.5 回归模型

• 回归模型可以用来近似给定的数据。

3.5.6 直方图

• 直方图使用分箱来近似数据分布
• 划分规则：
  • 等宽
    • 将范围划分为N个大小相等的间隔：均匀网格

3.5.7 聚类

​ 聚类技术把数据元组看做对象，将对象划分为群或簇，使得在一个簇中的对象相互“相似”，而与其他簇中的对象“相异”。通常，相似性基于距离函数。

3.5.8 抽样

• 抽样可以作为一种数据归约的技术使用。
• 抽样：允许用数据小得多的随机样本（子集）表示大型数据集。
• 关键原则：选择数据的一个代表性子集。
• 如果样本与原始数据具有近似相同的（感兴趣的）属性，则该样本具有代表性。
  • 简单随机抽样
  • 簇抽样
  • 分层抽样
• 抽样的方式
  • 简单随机抽样(SRS)：选择任何特定项目的概率都是相等的
  • 无放回简单随机抽样(SRSWOR)：一旦某个对象被选中，它将从群体中删除
  • 有放回简单随机抽样(SRSWR)：已选中的对象不从群体中移除

3.6 数据变换与数据离散化

• 标称数据转成one-hot编码

• 数据变换的策略：

  • 平滑：去除数据中的噪声。如分箱、聚类、回归。

  • 属性重构：通过现有属性构造新的属性，并添加到属性集中。

  • 规范化：将数据按比例缩放，使之落入一个小的特定区间。

    • 最小－最大规范化

      • 最小—最大值标准化保留了原有数据值的关系。

    • z-score规范化：基于属性A的平均值和标准差规范化。
      $$v^{\prime }=\frac{v-\overline{A}}{{\sigma }_A}$$
      其中$\overline{A}$和${\sigma }_A$是属性A的均值和标准差。 标准差可以用均值绝对偏差替换。

    • 小数定标规范化：通过移动属性A的小数点位置进行规 范化。
      $$v^{\prime }=\frac{v}{10^j}$$
      其中j是使得max(|v’|)<1的最小整数。

  • 离散化：用区间标签或概念标签替换。

    • 原因：易于组织成更高层次的概念；某些模型只能使用离散属性(决策树)
    • 决策树：结点{属性} 边{属性值} 叶子结点{类别}
    • 离散化将连续属性的范围划分为区间，通过区间标签可用来替换实际的数据值，通过离散化减少数据取值的个数。
    • 分箱

  • 概念分层：数据属性可以泛化得到较高的概念层。层次性地组织概念（如：属性值）

    • 概念层次结构的形成：通过收集较低级概念（如城市）并将其替换为较高级的概念（如省份等），可以减少数据取值的数量。

3.7 小结

第三章完