1、假设所分析的数据包括属性age，它在数据元组中的值（以递增序）为13 ,15 ,16 ,16 ,19 ,20 ,20 ,21 ,22 ,22 ,25 ,25 ,25 ,25 ,30 ,33 ,33 ,35 ,35 ,35 ,35 ,36 ,40, 45 ,46 ,52,70。

---

a. 该数据的均值是多少？中位数是什么？

使用R语言，首先存入数据

data <-c(13,15,16,16,19,20,20,21,22,22,25,25,25,25,30,33,33,35,35,35,35,36,40,45,46,52,70)

然后分别计算均值和中位数

mean_value <- mean(data)
median_value <- median(data)

结果如下：

b. 该数据的众数是什么？讨论数据的模态（即二模、三模等）。

众数为25和35，所以该数据是一个双峰的分布，即二模。

c. 该数据的中列数是多少？

中列数就是最大值与最小值的平均值

midrange <-(max(data) + min(data))/2

结果为41.5

d. 你能（粗略地）找出该数据的第一个四分位数（Q1）和第三个四分位数（Q3）吗？

可以使用quantile()计算分位数，第二个参数为0.25时是第一个四分位数，0.75时就是第三个四分位数

upper_quartile <- quantile(data,0.75)
lower_quartile <- quantile(data,0.25)

结果为：

e. 给出该数据的五数概括。

五数包括最小值、下四分位数、中位数、上四分位数与最大值，分别是13、20.5、25、35、70。

f. 绘制该数据的盒图。

可以使用R语言中的boxplot绘制盒图

boxplot(data, main="盒图", ylab="Age")

绘制结果如下，70为异常值，用°标出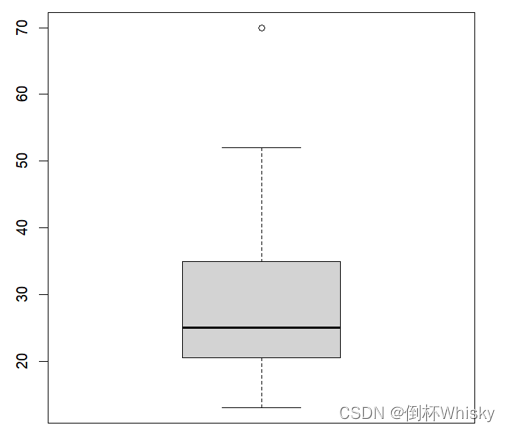

g. 分位数-分位数图与分位数图有何不同？

• 分位数图是一种图形方法，用于显示单变量分布中小于或等于自变量的值的近似百分比因此，它将显示所有数据的分位数信息，其中针对自变量测量的值将相对于其相应分位数进行绘制。
• 分位数-分位数图将一个单变量分布的分位数与另一单变量分布的相应分位数作图。两个轴均显示针对其相应分布的测量值范围，并绘制对应于两个分布的分位数的点。

2、在数据分析中，重要的选择相似性度量。然而，不存在广泛接受的主观相似性度量，结果可能因所用的相似性度量而异。虽然如此，在进行某种变换后，看来似乎不同的相似性度量可能等价。

	A1	A2
X1	1.5	1.7
X2	2	1.9
X3	1.6	1.8
X4	1.2	1.5
X5	1.5	1.0

---

a. 把该数据看做二维数据点。给定一个新的数据点x = (1.4,1.6) 作为查询点，使用 欧几里得距离、 曼哈顿距离、上确界距离和余弦相似性，基于查询点的相似性对数据库的点排位。

首先将数据存入data，并创建查询点query_point

data <- data.frame(
  X = c(1.5, 2, 1.6, 1.2, 1.5),
  Y = c(1.7, 1.9, 1.8, 1.5, 1.0)
)
query_point <- c(1.4, 1.6)

然后分别计算上面的几个指标

• 欧几里得距离

euclidean_distances <- sqrt((data$X - query_point[1])^2 + (data$Y - query_point[2])^2 )

• 曼哈顿距离

manhattan_distances <- abs(data$X - query_point[1]) + abs(data$Y - query_point[2])

• 上确界距离

chebyshev_distances <- pmax(abs(data$X - query_point[1]), abs(data$Y - query_point[2]))

• 余弦相似性

cosine_similarities <- rowSums(data * query_point) / (sqrt(rowSums(data^2)) * sqrt(sum(query_point^2)))

最后的结果：

基于距离，按照从近到远排位，对于余弦相似性，按从高到低排

b. 规格化该数据集，使得每个数据点的范数等于1。在变换后的数据上使用欧几里得距离对诸数据点排位。

相比于上一题多了一个规格化，把每个数据除以每个数据点的范数即可得到范数等于1
下面分别规格化数据点和查询点

# 规格化数据点
normalized_data <- data / sqrt(rowSums(data^2))
# 规格化查询点
normalized_query <- query_point / sqrt(sum(query_point^2))

然后计算欧几里得距离

euclidean_distances <- sqrt(rowSums((normalized_data - normalized_query)^2))

下面是进行排位后的结果

3、使用如下方法规范化如下数组： 200，300，400，600, 1000

a. 令 min=0，max=1，最小最大规范化。

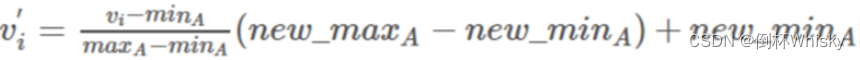
Original data	200	300	400	600	1000
normalized	0	0.125	0.25	0.5	1

b. z 分数规范化。

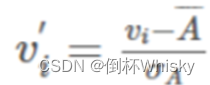
Original data	200	300	400	600	1000
normalized	-1.06	-0.7	-0.35	0.35	1.78

c. z 分数规范化，使用均值绝对偏差而不是标准差。

Original data	200	300	400	600	1000
normalized	-1.25	-0.83	-0.42	0.42	2.08

d. 小数定标规范化。

Original data	200	300	400	600	1000
normalized	0.2	0.3	0.4	0.6	0.1

4、假设12个销售价格记录已经排序，如下所示：
5，10，11，13，15，35，50，55，72，92，204，215
使用如下各方法将它们划分成三个箱。

---

a. 等频划分。

Bin1	5,10,11,13
Bin2	15,35,50,55
Bin3	72,92,204,215

b. 等宽划分。

Bin1	5,10,11,13,15,35,50,55,72
Bin2	92
Bin3	204,215

c. 聚类。

Bin1	5,10,11,13,15
Bin2	35,50,55,72,92
Bin3	204,215