简介

XFunction是一个基于qt和opengl开发的数学函数可视化工具。核心功能为空间直角坐标系下实值函数图像的绘制与观察，且支持时间参数（动态图像）。

前言

在学习了一些opengl相关的知识后总觉得有点纸上谈兵的感觉，所以想着做点东西熟悉和巩固一下，也是对学习opengl做一个阶段性记录。
思来想去就有了这么一个想法：做一个数学函数绘图工具，而且要做到偏极简风格，即使是一个初次接触的用户也可以在短短几十秒内熟悉它的功能更和用法。
鉴于直角坐标系下的函数图像绘制相对基础、简单，所以该工具以实现直角坐标系下的简单函数绘制为基础目标。
这篇文章不会完整叙述XFunction的所有开发内容，而是会着重介绍开发过程中遇到的一些难点和功能实现的思想；因此需要读者对qt与opengl有一定的基础。

函数

这里说的函数是指空间直角坐标系下的实值函数，以下简称函数。其一般形式为
$$z=f(x,y)$$
对于定义域上的任意 $(x,y)$ ，都有唯一的 $z$ 值与其对应。所以在三维直角坐标系下很多函数图像是一个曲面。

定义域网格

由于函数值的唯一性，每个点 $(x,y)$ 都只对应一个 $z$ 值，这就给了我一个启发：
首先我会生成一个正方形定义域网格 $(n+1)\times (n+1)$ （$n$为细分数，以下不作说明均为该含义），网格上的每一点都有一个位置的 $x$ 和 $y$ 值，我们就可以利用这个 $(x,y)$ 来计算该点处的函数值。我的想法很简单，生成一个单位平面上的点阵，在点阵上构建三角面。我们只要定义好定义域的必要信息（比如细分、尺寸）即可。在最终函数值的计算时也会用到这些信息，譬如说因为我定义的网格是单位网格，当计算某一点函数值时应当根据尺寸对该点坐标进行缩放，否则函数图像会永远只显示在 $[-1,1]\times [-1,1]$ 这个矩形区域上。
至于为什么要生成单位网格而不是实际尺寸的原因是尺寸会随时调整，如果每次用户调整尺寸都需要重新生成网格的话会产生较大的计算量，而且每次都要重新将内存中的数据传入gpu内存中也是消耗时间的。所以我选择使用单位网格并在着色器中对位置缩放，这样用户更改了尺寸并不会产生过多的额外计算与数据传输。
为了使用更少的数据，我会使用这个函数进行绘制：

void glMultiDrawElements(	GLenum mode, const GLsizei * count, GLenum type, const GLvoid * const * indices, GLsizei drawcount)

首先需要分配合适的内存空间：

    int row_n = domain_divs+1;
    if(domain_data == nullptr){
        domain_data = new float[int(2*pow(row_n,2))]();
        domain_inds = new unsigned[2*domain_divs*(domain_divs+1)]();
        domain_row_inds = new unsigned*[domain_divs];
        domain_row_pt_counts = new int[domain_divs]();
    }

$domain\_data$ 存储顶点数据，每个点2个坐标值：$(x,y)$，所以是 $2\ast row\_n^2$ (注意$row\_n=domain\_divs+1$)；
$domain\_inds$ 存储三角网格索引数据，我会使用如下所示的索引连接方式（此处 $n=3$）：

这样的话，每一行 $n+1$ 个点，形成一行三角网格需要 $2\ast (n+1)$ 个索引，总共需要n行，因此索引的分配数量是 $2\ast domain\_divs\ast (domain\_divs+1）$。
$domain\_row\_inds$ 是每一行三角网格的索引，因为我们已经存储在 $domain\_data$ 里面，后面只要设置好偏移量就行，所以一共需要 $domain\_divs$ 行。
$domain\_row\_pt\_counts$ 表示每行网格索引的点数量，容量也是 $domain\_divs$。
所有数据的计算与填充会是这样：

void XCommon::genDomainData(unsigned divs)
{
    if(divs != 0){
        domain_divs = divs;
        delete[] domain_data;
        domain_data = nullptr;
        delete[] domain_inds;
        domain_inds = nullptr;
        delete[] domain_row_inds;
        domain_row_inds = nullptr;
        delete[] domain_row_pt_counts;
        domain_row_pt_counts = nullptr;
    }
    int row_n = domain_divs+1;
    if(domain_data == nullptr){
        domain_data = new float[int(2*pow(row_n,2))]();
        domain_inds = new unsigned[2*domain_divs*(domain_divs+1)]();
        domain_row_inds = new unsigned*[domain_divs];
        domain_row_pt_counts = new int[domain_divs]();
    }

//    gen grid points----------------------
    for(int i=0; i<domain_divs+1; ++i){
        for(int j=0; j<domain_divs+1; ++j){
            int pos = 2 * (i*row_n + j);
            domain_data[pos] = 2*float(j)/domain_divs-1;    // x
            domain_data[pos+1] = 2*float(i)/domain_divs-1;    // y
        }
    }

//    gen all triangle strip indices---------------------
    for(int i=0; i<domain_divs; ++i){
        for(int j=0; j<domain_divs+1; ++j){
            int temp = i*row_n+j;
            domain_inds[2*temp] = temp;
            domain_inds[2*temp+1] = temp+row_n;
        }
    }

//    gen row inds-----------------
    for(int i=0; i<domain_divs; ++i)
        domain_row_inds[i] = static_cast<unsigned*>(0)+(2*i*row_n);


//    gen domain row pt counts----------------------
    for(int i=0; i<domain_divs; ++i)
        domain_row_pt_counts[i] = 2*row_n;
}

依次为内存分配 - 点位置信息计算 - 三角网格索引号计算 - 每行索引偏移量计算 - 每行点数量。
这样计算出来的点阵网格是平铺在单位矩形上的（$x,y\in [-1,1]$）。
之后像这样绘制网格：

    glMultiDrawElements(GL_TRIANGLE_STRIP, XCommon::domain_row_pt_counts, GL_UNSIGNED_INT, (void**)XCommon::domain_row_inds, XCommon::domain_divs);

需要注意的是虽然我们别无选择的绘制成三角网格，但是在逻辑上我们应当认为它是一个四边形网格，后面对于一些几何信息的计算也是当成四边网格来处理。

高度图

有了定义域网格就可以用顶点着色器来计算函数值，并将其设置为点位置的 $z$ 分量。但是这个想法很快就被否定，因为这样的话就是在顶点着色阶段改变了点的位置，该点处的法线无疑也会变化。而计算光照时法线信息是必不可少的，我们就需要想办法计算正确的法线。想要计算这样的网格上的法线信息必须要知道与其相邻的点的位置信息，更精确的说是 $z$ 值（因为生成的网格每一行每一列都是等距的，所以所有相邻点的 $x、y$ 值可以很容易计算）。再次强调，对于几何计算我会将三角网格当成四边网格来处理：

例如想象计算上图中间那个点处的法线，我的想法是首先得到与其相关的四个面的法线再取平均值，而面的法线可以简单的使用两条边的叉乘获得。因此，计算法线的必要信息就是当前点的所有邻接点的位置（$z$ 值）。换句话说我需要计算周围四个点的 $z$ 值才能计算当前点的法线。这会造成巨大的重复计算，故舍弃。
说到底，我想要的是点与其周围点的 $z$ 值，如果把这个值计算好并存储在一张纹理图中，重开一个shader设置好sampler2d参数不就可以拿到这些信息了吗。这样不仅可以设置点的 $z$ 值，亦可以拿到周围点的 $z$ 值并正确计算当前的的法线。于是有了新的思路：使用帧缓冲渲染出一个单色图（GL_R32F）。这个图存储了每一个定义域网格点的 $z$ 值，我们可以在片段着色器中计算当前 $(x,y)$ 处的 $z$ 值并输出。此处要注意的是 $(x,y)$ 需要根据网格尺寸转化成世界坐标：

#version 450 core

out float height;

layout(binding = 1) uniform FRAME_INFO{
    int w, h, domain_divs;
    float domain_w, domain_h, time;
};

float _calHeight(float x, float y){
    float res;
    return res;
}

void main(){
    vec2 suv = gl_FragCoord.xy / vec2(domain_divs+1,domain_divs+1);
    suv = (2*suv-1)*vec2(domain_w,domain_w);
    height = _calHeight(suv.x, suv.y);
    height = isinf(height)? (domain_h+10):(isnan(height)? (domain_h+10):height);
}

代码中的 $w,h$表示当前渲染窗口的分辨率，用以确定窗口上的点对应的单位坐标，$domain\_w,domain\_h$ 表示定义域网格的尺寸与最大值限制，$domain\_divs$ 表示网格的细分。而 _CalHeight 函数即为计算 $z$ 值的函数。同时需要处理一些函数值极端情况，否则会造成后期网格点消失。不用对_CalHeight函数体感到疑惑，这个函数的内容应当由用户输入，每提交一次输入都会更新这个shader将输入的数学函数添加到这个_CalHeight内。
以上输出的是一张函数 $z$ 值图，虽然opengl的坐标系中 $z$ 轴是面向屏幕的，但最后我会将其转化成向上的方向（$y$ 轴），所以称其为高度图。另外顶点着色器非常简单：

# version 450 core

layout (location = 0) in vec2 iP;

void main(){
    gl_Position = vec4(iP,0,1);
}

只需要传递一个由两个三角形组成的屏幕矩形的数据即可。
整个高度图的渲染代码看起来是这样的：

        // render height map------------------------
        XCommon::g_height_fbo->bind();
        glViewport(0, 0, XCommon::domain_divs+1, XCommon::domain_divs+1);
        glDisable(GL_DEPTH_TEST);
        glDisable(GL_BLEND);
        XCommon::g_screen_vao.bind();
        XShader::heightMap.use();
        glDrawArrays(GL_TRIANGLES, 0, 6);
        XCommon::g_height_fbo->release();

输出的高度图看起来会是这样的（以三角函数为例）：

GBuffer与法线

有了上述的高度图，我们几乎就有了完整函数图像的蓝图了，只需要把定义域网格根据高度图绘制出来即可。为了统一处理几何信息，我选择使用一个新的GBuffer帧缓冲并在新的shader里计算和输出最终网格的位置与法线，我更喜欢在观察空间中计算光照。所以会把位置、法线都转化到观察空间。这看起来会是这样：

void main(){
    ivec2 p = ivec2(gl_VertexID%(domain_divs+1), gl_VertexID/(domain_divs+1));
    float h = texelFetch(tex,p,0).x;
    gl_Position.xy = iP*vec2(domain_w,domain_w);
    gl_Position.z = h;
    gl_Position.w = 1;
    gl_Position = gl_Position.xzyw;
    gl_Position.z = -gl_Position.z;

    cout.P = vec3(view*gl_Position);
    cout.N = mat3(transpose(inverse(view)))*calN(gl_Position.y, p);
    gl_Position = proj*view*gl_Position;
    if(h>domain_h)
        gl_Position.z = gl_Position.w+10;
}

注意我没有使用常用的贴图采样函数，因为无法保证其精确度，转而使用将点编号转化成像素坐标直接读取像素值。其实就是有 ($domain\_divs+1)\ast (domain\_divs+1)$ 个点从一张分辨率为 ($domain\_divs+1)\ast (domain\_divs+1)$ 的图片中提取对应位置的像素值。同时会根据网格尺寸将坐标进行缩放（iP是输入顶点数据）。第7、8两行代码就是做一个坐标转换，转换后函数的 $z$ 轴会指向上方，$y$ 轴会指向屏幕里面，相当于把opengl的坐标系绕 $x$ 轴转了 $90°$。cout.P、cout.N就是要输出的几何信息，这里的重点是calN这个函数，它就是用来计算法线的：

vec3 calN(float ch, ivec2 p){
    float du = 2.*domain_w/domain_divs;
    vec3 res=vec3(0);
    vec3 d1 = vec3(-du,0,texelFetch(tex,p+ivec2(p.x==0?0:-1,0),0).x-ch);
    vec3 d2 = vec3(0,-du,texelFetch(tex,p+ivec2(0,p.y==0?0:-1),0).x-ch);
    vec3 d3 = vec3(du,0,texelFetch(tex,p+ivec2(p.x==domain_divs?0:1,0),0).x-ch);
    vec3 d4 = vec3(0,du,texelFetch(tex,p+ivec2(0,p.y==domain_divs?0:1),0).x-ch);

    res += cross(d1, d2);
    res += cross(d2, d3);
    res += cross(d3, d4);
    res += cross(d4, d1);
    res = res.xzy;
    res.z = -res.z;
    return normalize(res);
}

非常直观，取了周围4个点的高度并构造出边矢量，利用叉乘计算四个面的法线取平均值（单位化）。唯一需要注意的是当点在图片边缘时要处理旁边没有点的情况，否则会形成坏法线，也会影响光照效果：

计算好几何信息后传入片段着色器直接输出即可：

#version 450 core

layout(location = 0)out vec3 outP;
layout(location = 1)out vec3 outN;

in _cout{
    vec3 P;
    vec3 N;
}cin;

void main(){
    outP = cin.P;
    outN = cin.N;
}

渲染GBuffer的代码是这样的：

//    render gbuffer---------------------
    XCommon::g_gbuf_fbo->bind();
    glDisable(GL_BLEND);
    glDrawBuffers(XCommon::gbuf_attache_count, XCommon::gbuf_attaches);
    glViewport(0, 0, XCommon::glwid, XCommon::glhei);
    glEnable(GL_DEPTH_TEST);
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
    glPolygonMode(GL_BACK, GL_LINE);
    glPolygonMode(GL_FRONT, GL_FILL);
    glFrontFace(GL_CW);
    glActiveTexture(GL_TEXTURE0);
    glBindTexture(GL_TEXTURE_2D, XCommon::g_height_fbo->texture());
    XCommon::g_domain_vao.bind();
    XShader::gBuf.use();
    glMultiDrawElements(GL_TRIANGLE_STRIP, XCommon::domain_row_pt_counts, GL_UNSIGNED_INT, (void**)XCommon::domain_row_inds, XCommon::domain_divs);

绑定了高度图后使用glMultiDrawElements函数渲染即可。

函数渲染

到此，所有的东西都已经准备好了，我把它们都存储在GBuffer的颜色缓冲中。现在只需绑定好这些贴图，渲染一个屏幕矩形，在shader中计算光照就行了：

void main(){
    vec2 suv = gl_FragCoord.xy / vec2(w,h);
    vec3 P = texture2D(texP,suv,0).xyz;
    vec3 N = texture2D(texN,suv,0).xyz;
    vec3 scd = shadeLighting(P, N);
    cd = P==vec3(0)? vec4(0) : vec4(scd, 1);
    // cd = vec4(N,1);
    // cd = vec4(texture2D(texH,suv,0).xxx,1);
}

当采样到的位置为0时我们认为这是空白处。
对应的渲染代码如下：

//    render to screen--------------------------------
    glBindFramebuffer(GL_FRAMEBUFFER, defaultFramebufferObject());
    glDisable(GL_BLEND);
    glDisable(GL_DEPTH_TEST);
    glViewport(0, 0, XCommon::glwid, XCommon::glhei);
    glClear(GL_COLOR_BUFFER_BIT);
    glPolygonMode(GL_FRONT_AND_BACK, GL_FILL);

    glActiveTexture(GL_TEXTURE0);
    glBindTexture(GL_TEXTURE_2D, XCommon::g_gbuf_fbo->textures()[0]);
    glActiveTexture(GL_TEXTURE1);
    glBindTexture(GL_TEXTURE_2D, XCommon::g_gbuf_fbo->textures()[1]);
    glActiveTexture(GL_TEXTURE2);
    glBindTexture(GL_TEXTURE_2D, XCommon::g_height_fbo->textures()[0]);
    XCommon::g_screen_vao.bind();
    XShader::frameSampler.use();
    glDrawArrays(GL_TRIANGLES, 0, 6);

摄像机

摄像机是这个工具中一个比较重要的角色，所有的观察、视角变换都依赖它。

投影

首先简单介绍一下之后会用到的投影。

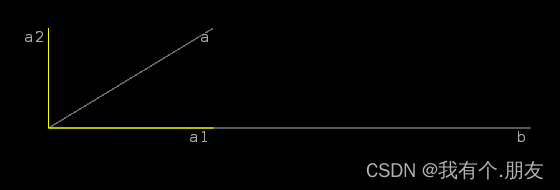
上图中 $a,b$ 为任意两个向量，黄色的 $a_1$ 为 $a$ 在 $b$ 上的的投影，我们定义 $a_2=a-a_1$ 为 $a$ 在 $b$ 上的法投影。
不难看出 $$a_1=|a|\cdot cos(\theta )\cdot \frac{b}{|b|}=\frac{a\cdot b}{b\cdot b}\cdot b$$ $$a_2=a-a_1=a-\frac{a\cdot b}{b\cdot b}\cdot b$$ 当 $b$ 为单位向量时还可化简为 $$a_1=(a\cdot b)\cdot b$$ $$a_2=a-(a\cdot b)\cdot b$$之所以称 $a_2$ 为法投影是因为 $a_2\perp b$（可自行证明）。

垂向量

这里给出一个向量的其中一个垂向量的推导过程。
设 $x=(x_1,x_2,x_3......x_n)$ 是 $n(n⩾2)$ 维空间中的任一向量，而 $y=(y_1,y_2,y_3......y_n)$ 是与其垂直的另一向量，于是有 $$x\cdot y=x_1\cdot y_1+x_2\cdot y_2+......+x_n\cdot y_n=0\text{\hspace{1em}(1)}$$为了让 $y$ 更简洁，我们令 $y_1=y_2=......=y_{n-1}=x_n$ ，此时(1)式为 $$x_1\cdot x_n+x_2\cdot x_n+......+x_{n-1}\cdot x_n+x_n\cdot y_n=0$$ 于是求出 $y_n=-x_1-x_2-......x_{n-1},(x_n\ne 0)$。即 $y=(x_n,x_n......x_n,-x_1-x_2-......-x_{n-1})$ 。但这是当 $x_n\ne 0$ 时成立的，我们需要单独考虑 $x_n=0$ 的情况。当 $x_n=0$ 时，$y$ 只有第 $n$ 个分量可能不为0，其余全为0，利用代数学的知识不难证明此时一定有 $x\cdot y=0$ ，因此我们有：
$$对于n(n⩾2)维空间中的一个向量x=(x_i{)}_{i=1}^n,它的其中一个垂向量是x^{\prime }=(x_n,x_n......x_n,-\sum _{i=1}^{n-1}{x}_i)$$
比如二维平面上的向量 $(x,y)\perp (y,-x)$，三维空间的向量 $(x,y,z)\perp (z,z,-x-y)$ 。

旋转

关于视角旋转我的想法是做到越容易理解越好，所以使用位置和方向来控制摄像机的变换：

    QVector3D P{0,0,0};    // position
    QVector3D dir{0,0,-1};    // front
    QVector3D right{1,0,0};    // right
    QVector3D up{0,1,0};    // up
    QVector3D wup{0,1,0};

当鼠标在窗口上拖动时可以利用qt的鼠标事件计算出滑行信息，再用这个信息计算视图应该如何旋转：

void XCamera::rotate(const float& rx, const float& ry, const float& rz, const int& rot_type)
{
    QQuaternion rotq = QQuaternion::fromAxisAndAngle(-dir, qRadiansToDegrees(-rz));
    rotq *= QQuaternion::fromAxisAndAngle(wup, qRadiansToDegrees(-ry));
    rotq *= QQuaternion::fromAxisAndAngle(right, qRadiansToDegrees(-rx));

//    update local axis----------------------
    dir = (rotq*dir).normalized();
    right = (rotq*right).normalized();
    up = QVector3D::crossProduct(right,dir).normalized();
}

这看起来很好，但是出于对计算机计算精度的担心，我认为我们只能信任一个方向。什么意思呢？ $dir$ 是可以信任的，但是 $right$ 不可信任，因为有可能计算出来的 $right$ 是不垂直于 $dir$ 的，也有可能 $right.y\ne 0$ 。所以我选择重新计算 $right$ ，使得 $dir\perp right,right.y=0$ ，这就要用到之前提到的知识了，我们知道 $dir\perp (dir.z,dir.z,-dir.x-dir.y)$ ，接着再计算 $right$ 在其上的投影即可。然而这样计算的结果仍有可能 $right.y\ne 0$ ，所以需要稍稍变一下，我们计算 $right$ 在 $(dir.z,0,-dir.x)$ 上的投影。这相当于把 $dir$ 投影到 $zx$ 平面上： $(dir.x,0,dir.z)$ ，接着在 $zx$ 平面上计算其垂向量得到 $(dir.z,0,-dir.x)$ （当成二维平面向量计算）。不难证明这个向量也是垂直于 $dir$ 的。并且其 $y$ 分量为0。

这里要注意的是我过多使用了向量的 $y$ 分量为0这个语句，然而这只在我们的摄像机没有发生滚转角的情况下才可用。因为XFunction设定上不会发生滚转，所以我可以大胆的使用这个语句。

经过修改的代码：

void XCamera::rotate(const float& rx, const float& ry, const float& rz, const int& rot_type)
{
    QQuaternion rotq = QQuaternion::fromAxisAndAngle(-dir, qRadiansToDegrees(-rz));
    rotq *= QQuaternion::fromAxisAndAngle(wup, qRadiansToDegrees(-ry));
    rotq *= QQuaternion::fromAxisAndAngle(right, qRadiansToDegrees(-rx));

//    update local axis----------------------
    dir = (rotq*dir).normalized();
    right = (rotq*right).normalized();
    if(dir.z()!=0 || dir.x()!=0){
        auto temp = QVector3D(dir.z(),0,-dir.x()).normalized();
        right = (QVector3D::dotProduct(right,temp)*temp).normalized();
    }
    up = QVector3D::crossProduct(right,dir).normalized();
}

这样我们就有理由相信旋转后摄像机坐标系依然是正交的。
到目前为止，旋转变换都是针对摄像机坐标系的，我想要的是整个场景会随着用户的交互而变换，不难想象到只要把摄像机位置也一起做变换不就行了吗：

void XCamera::rotate(const float& rx, const float& ry, const float& rz, const int& rot_type)
{
    QQuaternion rotq = QQuaternion::fromAxisAndAngle(-dir, qRadiansToDegrees(-rz));
    rotq *= QQuaternion::fromAxisAndAngle(wup, qRadiansToDegrees(-ry));
    rotq *= QQuaternion::fromAxisAndAngle(right, qRadiansToDegrees(-rx));

//    update local axis----------------------
    dir = (rotq*dir).normalized();
    right = (rotq*right).normalized();
    if(dir.z()!=0 || dir.x()!=0){
        auto temp = QVector3D(dir.z(),0,-dir.x()).normalized();
        right = (QVector3D::dotProduct(right,temp)*temp).normalized();
    }
    up = QVector3D::crossProduct(right,dir).normalized();
    
    if(rot_type == RotateByPivot)
        P = rotq*P;
}

看起来很好：

移动

摄像机移动有两种主要模式，一种是沿着摄像机朝向位移，另一种也是沿着摄像机朝向位移……说错了，另一种是沿着摄像机的 $right,up$ 位移。第一种看起来更像是缩放，第二种更像是移动。两种都没有特别之处，处理好看起来会是这样的：

定点变换

问题来了，我们所做的视图旋转有很大的局限，这个旋转始终都是以世界原点为中心进行变换的。当视图移动后，旋转会恢复到原点：

因此需要设置旋转中心点

        P = rot_piv+rotq*(P-rot_piv);

这个方法不错，但依然有问题，这涉及到旋转中心点与移动中心点的共同作用。如果你用这种方法实践过的话应该能感受到。
而我真正想要的是所谓的定点变换，意思是说在整个变换过程中始终有一个点相对于摄像机是始终不变的。
这会是这样的：

要实现这种效果稍微有点麻烦，我的想法是这样的：
当旋转中心点在原点且摄像机朝向原点时，原点就是定点。此时无论如何旋转，原点都不会改变，始终在窗口中心。依据这个线索再考虑当旋转中心点不在原点时我们应该像上述提到的方法这样处理

        P = rot_piv+rotq*(P-rot_piv);

这看起来已经把中心点定在了窗口中心（摄像机屏幕中心），问题是它会把摄像机的位置移动到错误的地方导致每次旋转都像重置了视图。这其实是因为我们的摄像机没有朝向那个定点。按照下面的方法可以有效解决：
想象一下我们首先将摄像机平移到其朝向定点，再去做各种旋转变换，最终再还原回来：

void XCamera::rotate(const float& rx, const float& ry, const float& rz, const int& rot_type)
{
    auto piv_off = (rot_piv-P)-QVector3D::dotProduct(rot_piv-P,dir)*dir;
    P += piv_off;

    QQuaternion rotq = QQuaternion::fromAxisAndAngle(-dir, qRadiansToDegrees(-rz));
    rotq *= QQuaternion::fromAxisAndAngle(wup, qRadiansToDegrees(-ry));
    rotq *= QQuaternion::fromAxisAndAngle(right, qRadiansToDegrees(-rx));

//    update local axis----------------------
    dir = (rotq*dir).normalized();
    right = (rotq*right).normalized();
    if(dir.z()!=0 || dir.x()!=0){
        auto temp = QVector3D(dir.z(),0,-dir.x()).normalized();
        right = (QVector3D::dotProduct(right,temp)*temp).normalized();
    }
    up = QVector3D::crossProduct(right,dir).normalized();

    if(rot_type == RotateByPivot)
        P = rot_piv+rotq*(P-rot_piv) - rotq*piv_off;
}

同样有一些需要注意的点，在移动摄像机时应沿着 $dir$ 在定点（$rot\_piv$）与摄像机位置（$P$）形成的向量上的法投影去位移；而在还原时应该使用变换矩阵作用一下之前的位移量（可能需要在脑海里模拟一下整个过程更有助于理解）。
剩下的就是定点移动了，这需要获取鼠标按下时对应的场景中的位置信息，并以这个位置为基准移动，我们需要两个信息：

    QVector3D rot_piv{0,0,0}, move_piv, move_ndc_piv;    // transform pivot

一个是世界空间中的定点、另一个是转换到屏幕空间的ndc坐标。整体的定点移动思路大概是这样的：
首先在鼠标（中键）按下时获取鼠标下的场景位置信息并存储到 $move\_piv$ 和 $move\_ndc\_piv$ 中，在鼠标拖动时将拖行位移单位化以匹配ndc坐标，接着把这段位移加到 $move\_ndc\_piv$ 中但是要保持深度信息不变（$move\_ndc\_piv.z$ 不变）；把这个新的 $move\_ndc\_piv$ 转化成世界坐标 $new\_move\_piv$ ，此时 $new\_move\_piv-move\_piv$ 就应该是这一点的位移量，我们只需要把它反向加到摄像机位置即可。这样的话就能保持鼠标下的点一直保持不变：

相对来说定点变换有一定的复杂度，需要多一点时间推测和理解。我这里描述的主要还是思路与逻辑，只要想明白了，按照逻辑去实现也只是时间问题。

场景

为了让场景看起来更佳有空间感我决定增加一个水平网格。它看起来是这样的：

这种网格看起来需要很多数据，实际上经过一番思考发现其实只需要极少的数据：

float XCommon::line_data[] = {
    // positions
    -1.0f,  1.f,
};

仅仅只是一个单位化的直线数据已经足够，我们完全可以使用 glDrawArraysInstanced 函数并在着色器中丰富它。一条直线，我们可以在顶点着色阶段把这它变换到周围的各个位置上使其充满水平面，一开始我想的是画出尽可能多的网格线（可能是 $2^{31}-1$ 条线），这样即使摄像机跑到很远的位置也不容易看见这个网格的边界。但很快就放弃了这个想法，因为这无疑是非常消耗性能的；不妨换个取巧的思路：
我们从当前摄像机位置处开始画，而且只画较少数量的网格，这样摄像机在任意位置都是在这个网格的中心处，并不会“觉得快要到了边界”。
事实证明这是可行的，我通过定义网格线的数量：

    static inline unsigned world_grid_divs{2+4*1024};

并在着色器中将其变换到中心点周围：

# version 450 core

layout (location = 0) in float iX;
out vec3 vP;

layout(binding = 0) uniform CAM_MAT{
    mat4 view, proj;
};

uniform int count=1;
uniform float unit_d = 1;
uniform vec2 cen = vec2(0);

void main(){
    int ind = gl_InstanceID;
    vec2 p = vec2(iX*(count*unit_d),0);
    p.y += ind<=1? 0 : (1-2*((ind>>1)%2))*((ind+2)/4)*unit_d;
    p = ind%2>0? p.yx:p;
    p += cen;
    gl_Position = proj*view*vec4(p.x,0,p.y,1);
    vP = vec3(view*vec4(p.x,0,p.y,1));
}

主函数的第3、4两行就是将其沿着两个坐标轴（$x,z$）推向周围。如果设置少一点数量就可以看出其工作原理了：

关于水平网格还有一个问题就是这个网格是正向渲染的，为了让它与GBuffer产生正确的透视关系我们需要将GBuffer的深度缓冲提取出来并应用到渲染网格的阶段，然而很快就会发现有严重的闪烁问题：

显然这是深度信息的交错造成的，为了解决这个问题，我决定不使用GBuffer的深度缓冲；而直接使用GBuFFer的位置信息（其实是因为qt中整合的深度缓冲无法采样，否则使用深度缓冲一样可行）。想法就是绘制网格时会与GBuffer的位置信息做深度判断，只有当网格的深度至少比GBuffer中的深度要近一小段距离时才会绘制网格，否则使其不可见：

#version 450 core

out vec4 cd;
in vec3 vP;

layout(binding = 1) uniform FRAME_INFO{
    int w, h, domain_divs;
    float domain_w, domain_h, time;
};
uniform sampler2D tex;

void main(){
    vec2 suv = gl_FragCoord.xy / vec2(w,h);
    float d=length(vP), sd=length(texture2D(tex,suv,0).xyz);
    // d = (sd==0? 1:(sd-d)>0.1*clamp(d*0.04,0.01,1)? 1:0)*0.3;
    d = (sd==0? 1:(sd-d>0.01? 1:0))*0.3;
    cd = vec4(1,1,1,d);
}

这样就能有效解决深度错乱闪烁问题：

场景的另一个物体就是坐标指示轴了，也就是上图中左下角的图标。这个坐标轴本身没有什么，只是用了三个轴向并应用了失去位移的观察矩阵即可，值得一提的是它的位置始终保持在左下方固定位置，并不会随着窗口大小而改变：

这是通过这些顶点着色器代码实现的：

    vec3 tp = iP*vec3(30./h);
    gl_Position = vec4(mat3(proj*view)*(tp)-vec3(1-85./w,1-85./h,0),1);

动态

XFunction的动态包含函数动态更新与时间参数的支持。
时间参数相对简单一些，就是每次渲染时更新着色器的时间变量即可。
函数动态更新是指当用户更新了数学函数后opengl的图像不会立即切换到新函数，而是有一个较为光滑的过度动画（gif比较影响帧率，大家看个意思就行）：

这看起来非常酷。而其背后的原理异常简单：
当一个数 $x$ 从 $a$ 变成 $b$ 时，我们怎样做才能让它有一个过度呢？答案是权重：$$x=t\cdot b+(1-t)\cdot a,t\in [0,1]$$ 式中的 $t$ 就是所谓的权重，可以看到参数 $t$ 完全控制了 $x$ 的行为，并且调节了其在 $a,b$ 之间的偏向程度。借着这个思路我很快联想到可以使用两个高度图，每当用户更新函数时开始做一个权重并控制两者之间的混合程度。这个想法很快被否定，因为不应该，不应该使用多余的高度图仅仅为了实现这个加分的效果，要知道多一张高度图可能就是多一张2k的图片渲染，这非常消耗算力。可以使用更简单稳妥的方法：混合！
当用户更新数学函数时触发如下函数：

void XGView::genHeightMap(const bool& need_anim)
{
    makeCurrent();
    if(need_anim && (! timer_update_heightmap->isActive()))
        timer_update_heightmap->start();

//    generate height map--------------------
    XCommon::g_height_fbo->bind();
    if(need_anim){
        glEnable(GL_BLEND);
        glBlendColor(1, 1, 1, sin((cur_height_blend_t-0.5)*M_PI)+1);
        glBlendFunc(GL_CONSTANT_ALPHA, GL_ONE_MINUS_CONSTANT_ALPHA);
    }
    else
        glDisable(GL_BLEND);
    glViewport(0, 0, XCommon::domain_divs+1, XCommon::domain_divs+1);
    glDisable(GL_DEPTH_TEST);

    XCommon::g_screen_vao.bind();
    XShader::heightMap.use();
    glDrawArrays(GL_TRIANGLES, 0, 6);
    XCommon::g_height_fbo->release();
    if(need_anim){
        if(cur_height_blend_t>1){
            timer_update_heightmap->stop();
            cur_height_blend_t = 0;
            is_update_fun = false;
        }
        else
            cur_height_blend_t += XCommon::height_blend_t;
    }
    update();
}

这个函数设置了一个三角混合系数（想象一下三角函数的形态，它会在极值点附近有着不错的缓入缓出效果），并且对这个系数增加了一个很小的值（XCommon::height_blend_t），同时会触发一个定时器，这个定时器设置的超时函数就是上面的函数，所以直到混合系数超过1才会停止混合。整个过程就是在混合时间段内高度图每次计算的高度信息是不变的、完整的，但是由于我们设置了混合，所以会以一个融合的效果融入上一次渲染的高度图，直到完整的过度成当前的高度信息图。

总结

目前该工具功能较单一，后续可能会有一些新的想法加入进去，比如根据参数方程或向量函数形式的可视化。